题目内容
【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.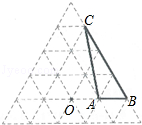
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
【答案】
(1)
解:如图,△A′B′C′为所作;
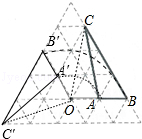
(2)
解:AB边旋转时扫过的面积=S扇形BOB′﹣S扇形AOA′
= ![]() ﹣
﹣ ![]()
=π.
【解析】(1)利用网格特点、等边三角形的性质和旋转的性质画出点A、B、C的对应点A′、B′、C,从而得到△A′B′C′;(2)根据扇形的面积公式,利用AB边旋转时扫过的面积=S扇形BOB′﹣S扇形AOA′进行计算即可.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )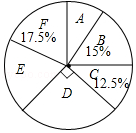
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人