题目内容
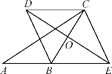
【题目】已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
【答案】见解析
【解析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,

∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.

练习册系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )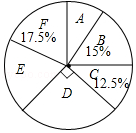
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人







