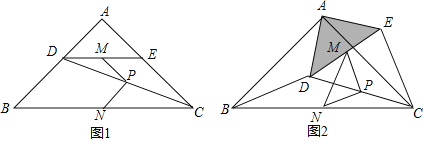
题目内容
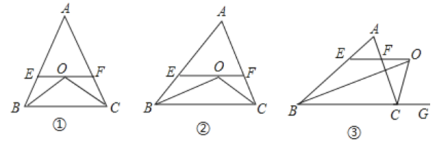
【题目】△ABC为等边三角形,O为BC的中点,D、E分别在边AB、AC上.如图1.
(1)若∠DOE=120°,求证:OD=OE;
(2)如图2,BD=4,CE=2,M是DE的中点,求OM的长.
【答案】(1)证明见解析;(2)MO![]() .
.
【解析】
(1)根据题意以O为圆心,OD长为半径画弧,交AB于点H,连接OH,则OH=OD,根据△ABC为等边三角形,∠DOE=120°,可知∠OEC=∠ADO,则可证出△BHO≌△CEO,可得OH=OE,即OD=OE;
(2)由题意连接BE,取BE的中点G,连接MG并延长交BC于点H,连接GO,过点O作OJ垂直MH,M为DE中点,G为BE中点,则MG∥DB,MG=![]() DB,∠MHO=∠ABC=60°,点O为BC的中点,点G为BE的中点,则GO∥EC,GO=
DB,∠MHO=∠ABC=60°,点O为BC的中点,点G为BE的中点,则GO∥EC,GO=![]() EC=1,∠GOH=∠C=60°,可推出HG=HO=GO=1,GJ=
EC=1,∠GOH=∠C=60°,可推出HG=HO=GO=1,GJ=![]() ,OJ=
,OJ=![]() ,在Rt△MOJ中,(
,在Rt△MOJ中,(![]() )2+(
)2+(![]() )2=MO2,解得MO=
)2=MO2,解得MO=![]() .
.
解:(1)如图1所示,
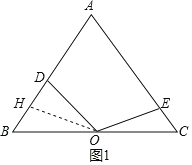
以O为圆心,OD长为半径画弧,交AB于点H,连接OH,则OH=OD.
∵△ABC为等边三角形,
∴∠B=∠C=∠A=60°,
∵∠DOE=120°,
∴∠A+∠DOE=180°,
∴∠ADO+∠AEO=180°,
∵∠OEC+∠AEO=180°,
∴∠OEC=∠ADO,
∵∠HDO=∠DHO,
∴∠BHO=∠ADO=∠OEC,
∵O为BC的中点,
∴BO=OC,
∴△BHO≌△CEO(AAS),
∴OH=OE,
∴OD=OE.
(2)如图2所示,
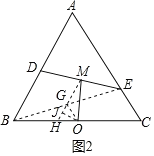
连接BE,取BE的中点G,连接MG并延长交BC于点H,连接GO,过点O作OJ垂直MH.
∵M为DE中点,G为BE中点,
∴MG∥DB,MG![]() DB=2,
DB=2,
∴∠MHO=∠ABC=60°,
∵点O为BC的中点,点G为BE的中点,
∴GO∥EC,GO![]() EC=1,
EC=1,
∴∠GOH=∠C=60°,
△GOH为等边三角形,
∴HG=HO=GO=1,
∴GJ![]() ,OJ
,OJ![]() ,
,
在Rt△MOJ中,
(![]() )2+(
)2+(![]() )2=MO2,
)2=MO2,
解得:MO![]() .
.

【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件数如下:
每人加工零件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件的平均数、中位数和众数;
(2)生产部负责人要定出合理的每人每月生产定额,你认为应该定为多少件合适?