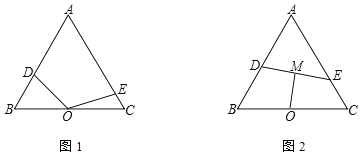题目内容
【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b![]() )2=0.
)2=0.
(1)求a,b的值;
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
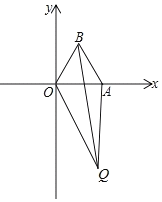
【答案】(1)a=1,b![]() ;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2
;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;当∠OQA=150°时,△AOQ的面积的最大值为2
;当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.
【解析】
(1)由题意根据完全平方式的非负性,即可求得a和b的值;
(2)根据题意易证△OAB为等边三角形,故可通过把△ABQ绕点A逆时针旋转60°得△AOC,把已知的QO=m、QA=n、QB=p统一到△OCQ中,得到△OCQ是直角三角形,再加上旋转得到的∠AQC=60°,即能求出∠OQA的度数;但由于不确定点Q的位置,故需分点Q在△OAB内部和点Q在△OAB外部两种情况讨论计算;
(3)由题意通过构造OQ边上的高AH求得△AOQ面积的表达式,根据条件给的不等式可知,当a=b时,ab可取得最大值为a2+b2,即OQ=AQ时,△AOQ取得最大值;根据勾股定理把AQ=OQ求出,即求出面积最大值;由于在(2)的条件下不确定∠OQA的度数,故需分两种情况讨论计算.
解:(1)∵1﹣2a+a2+(b![]() )2=0,
)2=0,
∴(1﹣a)2+(b![]() )2=0,
)2=0,
∴1﹣a=0,b![]() 0,
0,
∴a=1,b![]() .
.
(2)∵OA=2即A(2,0),B(1,![]() ),
),
∴OB![]() ,AB
,AB![]() ,
,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°,
把△ABQ绕点A逆时针旋转60°得△AOC,连接CQ,
∴∠CAQ=∠OAB=60°,AC=AQ=n,OC=BQ=p,
∴△ACQ是等边三角形,
∴CQ=AQ=n,∠AQC=60°,
∵p2=m2+n2即OC2=OQ2+CQ2,
∴△OCQ是直角三角形,∠OQC=90°,
①若点Q在△OAB的外部,如图1,
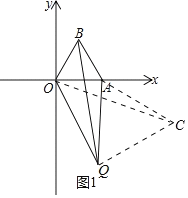
则∠OQA=∠OQC﹣∠AQC=90°﹣60°=30°;
②若点Q在△OAB的内部,如图2,
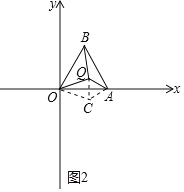
则∠OQA=∠OQC+∠AQC=90°+60°=150°,
综上所述:∠OQA的度数为30°或150°.
(3)∵a2+b2≥2ab,
∴当a=b时,a2+b2=2ab成立,即此时ab取得最大值,
过点A作AH⊥OQ于H,如图3,
∴∠AHQ=90°,
∵∠AQH=30°,
∴AH![]() AQ
AQ![]() n,
n,
∴S△AOQ![]() OQAH
OQAH![]() m
m![]() n
n![]() mn,
mn,
∴当m=n时,S△AOQ取得最大值![]() ,
,
①当∠OQA=30°时,如图3.
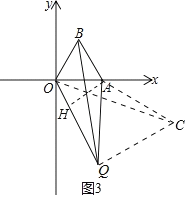
∵OQ=AQ=n,QH![]() ,
,
∴OH=OQ﹣QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ;
;
②当∠OQA=150°时,如图4,
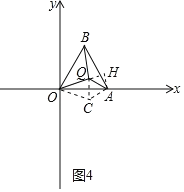
∴OH=OQ+QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ,
,
综上所述:当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;
;
当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.