题目内容
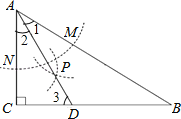
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
【答案】A
【解析】
试题分析:①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
③利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
④根据直角三角形的性质得出AD=2CD,再由线段垂直平分线的性质得出AD=BD,进而可得出结论.
解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
∵∠2=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∴BD=2CD.
故④正确.
故选A.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目