题目内容
【题目】阅读下面材料:
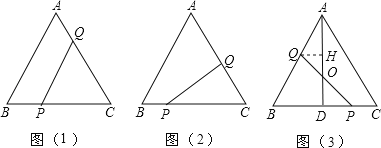
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求 ![]() 的值.
的值.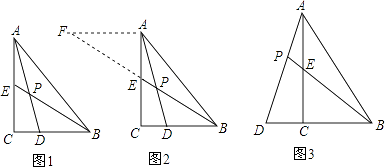
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
请回答: ![]() 的值为 .
的值为 .
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
①求 ![]() 的值;
的值;
(3)②若CD=2,则BP= .
【答案】
(1)![]()
(2)过点A作AF∥DB,交BE的延长线于点F,如图,
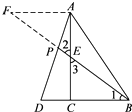
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
在△AEF和△CEB中,
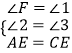 ,
,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴ ![]() 的值为
的值为 ![]()
(3)6
【解析】解:(1) ![]() 的值为
的值为 ![]() .
.
提示:易证△AEF≌△CEB,则有AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
由AF∥BC可得△APF∽△DPB,
即可得到 ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() ;
;
·(3)②当CD=2时,BC=4,AC=6,
∴EC= ![]() AC=3,EB=
AC=3,EB= ![]() =5,
=5,
∴EF=BE=5,BF=10.
∵ ![]() =
= ![]() (已证),
(已证),
∴ ![]() =
= ![]() ,
,
∴BP= ![]() BF=
BF= ![]() ×10=6.
×10=6.
所以答案是6.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目