题目内容
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡: ①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算. 
【答案】
(1)解:由题意可得:银卡消费:y=10x+150,普通消费:y=20x
(2)解:由题意可得:当10x+150=20x,
解得:x=15,则y=300,
故B(15,300),
当y=10x+150,x=0时,y=150,故A(0,150),
当y=10x+150=600,
解得:x=45,则y=600,
故C(45,600);
(3)解:如图所示:由A,B,C的坐标可得:
当0<x<15时,普通消费更划算;
当x=15时,银卡、普通票的总费用相同,均比金卡合算;
当15<x<45时,银卡消费更划算;
当x=45时,金卡、银卡的总费用相同,均比普通票合算;
当x>45时,金卡消费更划算.
【解析】(1)根据银卡售价150元/张,每次凭卡另收10元,以及旅游馆普通票价20元/张,设游泳x次时,分别得出所需总费用为y元与x的关系式即可;(2)利用函数交点坐标求法分别得出即可;(3)利用(2)的点的坐标以及结合得出函数图象得出答案.

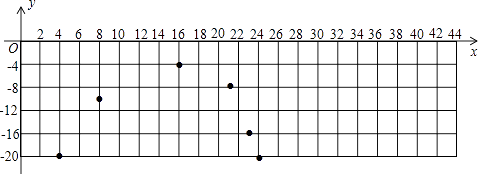
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至﹣20℃时,制冷再次停止,…,按照以上方式循环进行. 同学们记录了44min内15个时间点冷柜中的温度y(℃)随时间x(min)的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数. ①当4≤x<20时,写出一个符合表中数据的函数解析式;
②当20≤x<24时,写出一个符合表中数据的函数解析式;
(2)a的值为;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当4≤x≤44时温度y随时间x变化的函数图象.