题目内容
【题目】在△ABC中，∠B=∠C，AB垂直平分线与AC所在直线相交所得锐角为 50°，求∠B的大小.
【答案】70°或20°.
【解析】
根据△ABC中∠A为锐角与钝角分为两种情况，当∠A为锐角时，∠B等于70°，当∠A为钝角时，∠B等于20°.
根据△ABC中∠A为锐角与钝角，分为两种情况：
①如图：当∠A为锐角时，
∵AB的垂直平分线与AC所在的直线相交所得到锐角为50°，
∴∠A=40°，
∵∠B=∠C，∠A+∠B+∠C=180°，
∴∠B=
（180°-50°）=70°.
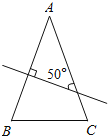
②当∠A为钝角时，如图：
∵AB的垂直平分线与AC所在的直线相交所得到锐角为50°，
∴∠1=40°，
∴∠BAC=140°，
∵∠B=∠C，∠1=∠B+∠C，
∴∠B=20°.
阅读快车系列答案
【题目】表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案．此公司每个月收取通话费与月租费的方式如下：若通话费超过月租费，只收通话费；若通话费不超过月租费，只收月租费．若小洁每个月的通话费均为x元，x为400到600之间的整数，则在不考虑其他费用并使用两年的情况下，x至少为多少才会使得选择乙方案的总花费比甲方案便宜？（ ）
甲方案 | 乙方案 | |
门号的月租费（元） | 400 | 600 |
MAT手机价格（元） | 15000 | 13000 |
注意事项：以上方案两年内不可变更月租费 | ||
A.500
B.516
C.517
D.600
【题目】已知y是x的函数，自变量x的取值范围x＞0，下表是y与x的几组对应值：
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
下面是小腾的探究过程，请补充完整：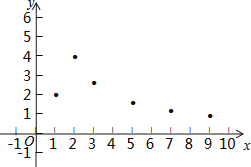
（1）如图，在平面直角坐标系xOy中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（2）根据画出的函数图象，写出：
①x=4对应的函数值y约为
②该函数的一条性质：