ЬтФПФкШн
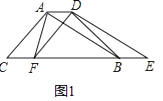
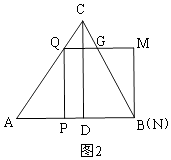
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC=5ЃЌABБпЩЯЕФИпCD=4ЃЌЕуPДгЕуAГіЗЂЃЌбиABвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуBдЫЖЏЃЌЕБЕуPВЛгыЕуAЁЂBжиКЯЪБЃЌЙ§ЕуPзїPQЁЭABЃЌНЛБпACЛђБпBCгкЕуQЃЌвдPQЮЊБпЯђгвВрзїе§ЗНаЮPQMNЃЎЩше§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЈЦНЗНЕЅЮЛЃЉЃЌЕуPдЫЖЏЕФЪБМфЮЊtЃЈУыЃЉЃЎ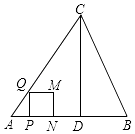
ЃЈ1ЃЉжБНгаДГіtanBЕФжЕЮЊ ЃЎ
ЃЈ2ЃЉЧѓЕуMТфдкБпBCЩЯЪБtЕФжЕЃЎ
ЃЈ3ЃЉЕБе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЮЊЫФБпаЮЪБЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉБпBCНЋе§ЗНаЮPQMNЕФУцЛ§ЗжЮЊ1ЃК3СНВПЗжЪБЃЌжБНгаДГіtЕФжЕЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ2
ЃЈ2ЃЉНтЃКЕБЕуMТфдкBCБпЩЯЪБЃЌШчЭМ1ЃЌ
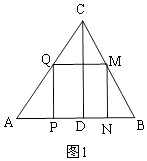
гЩЬтвтЕУЃКAP=3tЃЌ
tanЁЯCAB= ![]() ЃЌ
ЃЌ
ЁрPQ=PN=MN=4tЃЌBN=2tЃЌ
Ёр3t+4t+2t=5ЃЌ
t= ![]()
ЃЈ3ЃЉНтЃКЗжШ§жжЧщПіЃК
ЂйЕБ0ЃМtЁм ![]() ЪБЃЌШчЭМ1ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЌ
ЪБЃЌШчЭМ1ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЌ
ЁрS=PQ2=ЃЈ4tЃЉ2=16t2ЃЛ
ЂкЕБNгыBжиКЯЪБЃЌШчЭМ2ЃЌ
AP=3tЃЌPQ=PB=4tЃЌ
Ёр3t+4t=5ЃЌ
t= ![]() ЃЌ
ЃЌ
ЕБ ![]() ЃМtЃМ
ЃМtЃМ ![]() ЪБЃЌШчЭМ3ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧЮхБпаЮEQPNFЃЌ
ЪБЃЌШчЭМ3ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧЮхБпаЮEQPNFЃЌ
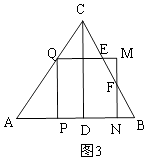
ЂлЕБ ![]() ЁмtЃМ1ЪБЃЌШчЭМ4ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧЬнаЮEQPBЃЌ
ЁмtЃМ1ЪБЃЌШчЭМ4ЃЌе§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЪЧЬнаЮEQPBЃЌ

ЁрAP=3tЃЌPN=4tЃЌ
ЁрBN=7tЉ5ЃЌPB=4tЉЃЈ7tЉ5ЃЉ=Љ3t+5ЃЌ
дкRtЁїAPQжаЃЌAQ=5tЃЌ
ЁрQC=5Љ5tЃЌ
ЁпAC=ABЃЌ
ЁрЁЯACB=ЁЯABCЃЌ
ЁпQEЁЮABЃЌ
ЁрЁЯQEC=ЁЯABCЃЌ
ЁрЁЯQEC=ЁЯACBЃЌ
ЁрQE=QC=5Љ5tЃЌ
ЁрS=SЬнаЮQPBE= ![]() ЃЈQE+PBЃЉЁСPQЃЌ
ЃЈQE+PBЃЉЁСPQЃЌ
= ![]() ЃЈ5Љ5t+5Љ3tЃЉЁС4t=Љ16t2+20tЃЛ
ЃЈ5Љ5t+5Љ3tЃЉЁС4t=Љ16t2+20tЃЛ
злЩЯЫљЪіЃЌSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃК
S= 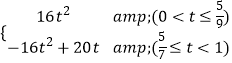
ЃЈ4ЃЉНтЃКШчЭМ2ЃЌЕБt= ![]() ЪБЃЌCQ=QG=5Љ5t=
ЪБЃЌCQ=QG=5Љ5t= ![]() ЃЌ
ЃЌ
ЁрGM=4tЉ ![]() =
= ![]() ЃЌ
ЃЌ
ЁрQG=GMЃЌ
ЁрSЁїQGB=SЁїGMBЃЌ
ЁрSЬнаЮGQPBЃКSЁїGMB=3ЃК1ЃЌ
ЕБPгыDжиКЯЪБЃЌt=1ЃЌШчЭМ5ЃЌ
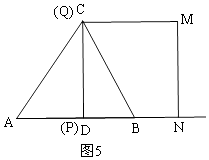
дђSЁїCDBЃКSЫФБпаЮCBNM= ![]() ЁС2ЁС4ЃКЃЈ42Љ
ЁС2ЁС4ЃКЃЈ42Љ ![]() ЁС2ЁС4ЃЉЃЌ
ЁС2ЁС4ЃЉЃЌ
=1ЃК3ЃЌ
злЩЯЫљЪіЃЌt= ![]() sЛђ1sЪБЃЌБпBCНЋе§ЗНаЮPQMNЕФУцЛ§ЗжЮЊ1ЃК3СНВПЗж
sЛђ1sЪБЃЌБпBCНЋе§ЗНаЮPQMNЕФУцЛ§ЗжЮЊ1ЃК3СНВПЗж
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЁпCDЁЭABЃЌ
ЁрЁЯADC=ЁЯADB=90ЁуЃЌ
ЁпдкRtЁїACDжаЃЌAD= ![]() =3ЃЌ
=3ЃЌ
ЁрBD=ABЉAD=5Љ3=2ЃЌ
ЁрдкRtЁїBCDжаЃЌtanЁЯB= ![]() =
= ![]() =2ЃЛ
=2ЃЛ
ЫљвдД№АИЪЧ2ЃЎ
ЁОПМЕуОЋЮіЁПЭЈЙ§СщЛюдЫгУЙДЙЩЖЈРэЕФИХФюКЭе§ЗНаЮЕФаджЪЃЌеЦЮежБНЧШ§НЧаЮСНжБНЧБпaЁЂbЕФЦНЗНКЭЕШгкаББпcЕФЦНЗН,МД;a2+b2=c2ЃЛе§ЗНаЮЫФИіНЧЖМЪЧжБНЧЃЌЫФЬѕБпЖМЯрЕШЃЛе§ЗНаЮЕФСНЬѕЖдНЧЯпЯрЕШЃЌВЂЧвЛЅЯрДЙжБЦНЗжЃЌУПЬѕЖдНЧЯпЦНЗжвЛзщЖдНЧЃЛе§ЗНаЮЕФвЛЬѕЖдНЧЯпАбе§ЗНаЮЗжГЩСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЛе§ЗНаЮЕФЖдНЧЯпгыБпЕФМаНЧЪЧ45oЃЛе§ЗНаЮЕФСНЬѕЖдНЧЯпАбетИіе§ЗНаЮЗжГЩЫФИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮМДПЩвдНтД№ДЫЬтЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ