题目内容
【题目】如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠点.D的对应点为D′. 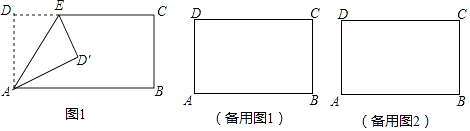
(1)求点D′刚好落在对角线AC上时,D′C的长;
(2)求点D′刚好落在此对称轴上时,线段DE的长.
【答案】
(1)解:如图1,在Rt△ABC中,
∵∴AD′=AD=5,
∵AC= ![]() =
= ![]() =
= ![]() ,
,
∴CD′=AC﹣AD′= ![]() ﹣5
﹣5
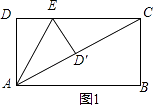
(2)解:①当D′落在对称轴GH上,
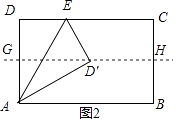
∵GH是矩形对称轴,
∴AC= ![]() AD,
AD,
由翻折的性质得:AD′=AD,∠DAE= ![]() ∠DAD′,
∠DAD′,
∴GA= ![]() AD′,
AD′,
∴在Rt△AGD′中,∠GAD′=60°,
∴∠DAE= ![]() ∠DAD′=30°,
∠DAD′=30°,
在Rt△ADE中,
∵tan∠DAE= ![]() ,即:tan30°=
,即:tan30°= ![]() ,
,
∴DE= ![]() ,
,
②当D′落在对称轴MN上,又分两种情况,
第一种:点E在DC上,如图3,
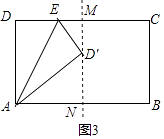
∵MN是矩形对称轴,
∴DM=AN=4,
由翻折得:AD′=AD,
在Rt△AND′中,
D′N= ![]() =3,
=3,
∴D′M=MN﹣D′N=5﹣3=2,
设DE=ED′=x,
在Rt△EAD′中,
ED′2=EM2+MD′2,
即:x2=(4﹣x)2+22,
解之得:x= ![]() ,即DE=
,即DE= ![]() ,
,
第二种:点E在DC延长线上,如图4,方法同上,DE=10.

综上所述,点D′落在矩形对称轴上时,DE的长为 ![]() 或
或 ![]() 或10.
或10.
【解析】(1)如图1,在Rt△ABC中,根据勾股定理即可得到结论;(2)①当D′落在对称轴GH上,由翻折的性质得到AD′=AD,∠DAE= ![]() ∠DAD′,求得GA=
∠DAD′,求得GA= ![]() AD′,根据三角形的内角和得到∠DAE=
AD′,根据三角形的内角和得到∠DAE= ![]() ∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N=
∠DAD′=30°,根据三角函数的定即可得到结论;②当D′落在对称轴MN上,又分两种情况,第一种:点E在DC上,如图3,得到DM=AN=4,由翻折的性质得到AD′=AD,在Rt△AND′中,由勾股定理得到D′N= ![]() =3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE=
=3,得到D′M=MN﹣D′N=5﹣3=2,设DE=ED′=x,在Rt△EAD′中,根据勾股定理得到DE= ![]() ,第二种:点E在DC延长线上,同理得到结论.
,第二种:点E在DC延长线上,同理得到结论.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

 优加精卷系列答案
优加精卷系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?