题目内容
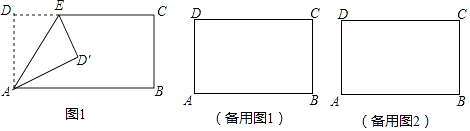
【题目】如图,抛物线y1=﹣ax2+2ax﹣a﹣3(a>0)和y2=a(x+1)2﹣1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
(1)①函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是;
②当y1、y2的值都随x的增大而增大时,自变量x的取值范围是;
(2)当EF=MN时,求a值,并判断四边形EMFN是何种特殊的四边形;
(3)若y2=a(x+1)2﹣1(a>0)的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程a(x+1)2﹣1=0的解.
【答案】
(1)-3;﹣1≤x≤1
(2)
解:∵y1=﹣a(x﹣1)2﹣3,y2=a(x+1)2﹣1,
∴N(﹣1,﹣1),M(1,﹣3).
由两点间的距离公式可知:MN=2 ![]() .
.
令x=0得:y1=﹣a﹣3,y2=a﹣1.
∴F(0,a﹣1),E(0,﹣a﹣3).
∴EF=2a+2.
∵EF=MN,
∴2a+2=2 ![]() ,解得:a=
,解得:a= ![]() ﹣1.
﹣1.

作NC⊥y轴于C,MD⊥y轴于D
∴NC=1,FC=a,MD=1,DE=a
∵在Rt△CNF和Rt△MDE中,  ,
,
∴△NCF≌MDE.
∴NF=EM,∠NFC=∠DEM
∴NF‖EM
∴四边形EMFN是平行四边形
又∵NM=EF
∴四边形EMFN是矩形
(3)
解:∵A(m,0)M(1,﹣3)N(﹣1,﹣1),
∴AN2=m2+2m+2,AM2=m2﹣2m+10,MN2=8.
①若AN=AM,则m2+2m+2=m2﹣2m+10,解得:m=2,
∴方程a(x+1)2﹣1=0的一个解为x=2,
根据抛物线对称性,可知方程的另一个解为x=﹣4.
②若AN=MN,则m2+2m+2=8,解得:m=﹣1+ ![]() 或m=﹣1﹣
或m=﹣1﹣ ![]() (舍去),
(舍去),
所以方程a(x+1)2﹣1=0的一个解为x=﹣1+ ![]() ,
,
根据抛物线对称性,可知方程的另一个解为x=﹣1﹣ ![]() .
.
③若AM=MN,所以m2﹣2m+10=8,
此方程无解,所以此种情况不成立
综上所述当△AMN为等腰三角形时,方程a(x+1)2﹣1=0的解为x1=2,x2=﹣4或x1=﹣1 ![]() 或x2=﹣1﹣
或x2=﹣1﹣ ![]()
【解析】解:(1)①y1=﹣ax2+2ax﹣a﹣3=﹣a(x2﹣2x+1)﹣3=﹣a(x﹣1)2﹣3,
∴函数y1=﹣ax2+2ax﹣a﹣3(a>0)的最大值是﹣3.
所以答案是:﹣3.
②∵y1=﹣a(x﹣1)2﹣3,﹣a<0,
∴当x≤1时,y随x的增大而增大.
∵y2=a(x+1)2﹣1(a>0),
∴当x≥﹣1时,y随x的增大而增大.
∴当﹣1≤x≤1时,y1、y2的值都随x的增大而增大.
【考点精析】利用二次函数的概念和二次函数的最值对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

 阅读快车系列答案
阅读快车系列答案【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
【题目】随着北京公交票制票价调整,公交集团换成了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版公交站牌每一个站名上方都有一个对应的数,将上下车站站名所对应数相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体内容如下:

乘车路程计价区段 | 0~10 | 11~15 | 16~20 | … |
对应票价(元) | 2 | 3 | 4 | … |
另外,一卡通普通卡刷卡实行五折优惠,学生卡实行二五折优惠.小明用学生卡乘车,上车时站名上对应的数是5,下车时站名上对应的数是22,那么小明乘车的费用是_____元.