题目内容
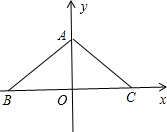在△ABC中，∠BAC=120°，AB=AC，BC=4，建立如下图的平面直角坐标系，则A、B、C个点的坐标分别是；A________、B________、C________．
（0，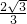
） （-2，0） （2，0）
分析：根据∠BAC=120°，AB=AC，OA⊥BC，可知：OB=OC=
BC，∠CAO=∠BAC．
在Rt△AOC中，可求OA的长，进而写出点A、B、C的坐标．
解答：∵∠BAC=120°，AB=AC，OA⊥BC，BC=4，
∴OB=OC=BC=2，∠CAO=∠BAC=60°．
在Rt△AOC中，OA=cot∠CAO×OC=
×2=
．
∴A（0，），B（-2，0），C（2，0）．
点评：本题主要考查解直角三角形．在解题过程中注意数形结合确定点的坐标．
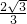） （-2，0） （2，0）分析：根据∠BAC=120°，AB=AC，OA⊥BC，可知：OB=OC=
BC，∠CAO=∠BAC．在Rt△AOC中，可求OA的长，进而写出点A、B、C的坐标．
解答：∵∠BAC=120°，AB=AC，OA⊥BC，BC=4，
∴OB=OC=
BC=2，∠CAO=∠BAC=60°．在Rt△AOC中，OA=cot∠CAO×OC=
×2=．∴A（0，
），B（-2，0），C（2，0）．点评：本题主要考查解直角三角形．在解题过程中注意数形结合确定点的坐标．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
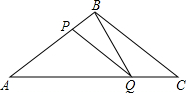；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以4cm/s的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以每秒4cm，的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．