Question

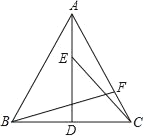
【题目】如图，CD⊥AB，EF⊥AB，垂足分别为D、F，∠1＝∠2，若∠A＝65°，∠B＝45°，求∠AGD的度数．

Answer 1

【答案】70°

【解析】

由CD⊥AB，EF⊥AB可得出∠CDF=∠EFB=90°，利用“同位角相等，两直线平行”可得出CD∥EF，利用“两直线平行，同位角相等”可得出∠DCB=∠1，结合∠1=∠2可得出∠DCB=∠2，利用“内错角相等，两直线平行”可得出DG∥BC，利用“两直线平行，同位角相等”可得出∠ADG的度数，在△ADG中，利用三角形内角和定理即可求出∠AGD的度数.

解：∵CD⊥AB，EF⊥AB，

∴∠CDF＝∠EFB＝90°，

∴CD∥EF，

∴∠DCB＝∠1．

∵∠1＝∠2，

∴∠DCB＝∠2，

∴DG∥BC，

∴∠ADG＝∠B＝45°．

又∵在△ADG中，∠A＝65°，∠ADG＝45°，

∴∠AGD＝180°﹣∠A﹣∠ADG＝70°