题目内容
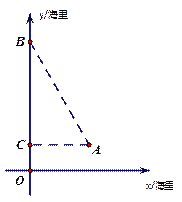
(本小题满分14分)如图9,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=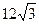 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以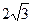 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
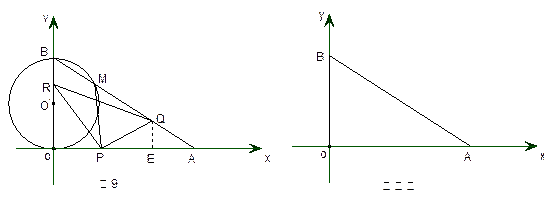
(1)求∠OAB的度数.
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
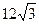 cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以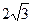 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
(1)求∠OAB的度数.
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
(1)∠OAB=30°
(2)t=3时,PM与⊙O‘相切
(3)

(4)当t=2,t=3.6,t=
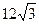 -18时,△APQ是等腰三角形.
-18时,△APQ是等腰三角形.解:(1)在Rt△AOB中:
tan∠OAB=
∴∠OAB=30°
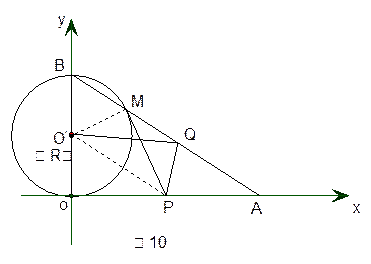
(2)如图10,连接O‘P,O‘M. 当PM与⊙O‘相切时,有∠PM O‘=∠PO O‘=90°,
△PM O‘≌△PO O‘
由(1)知∠OBA=60°
∵O‘M= O‘B
∴△O‘BM是等边三角形
∴∠B O‘M=60°可得∠O O‘P=∠M O‘P=60°
∴OP=" O" O‘·tan∠O O‘P =6×tan60°=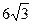
又∵OP=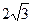 t
t
∴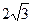 t=
t=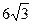 ,t=3
,t=3
即:t=3时,PM与⊙O‘相切.
(3)如图9,过点Q作QE⊥x于点E
∵∠BAO=30°,AQ=4t
∴QE= AQ=2t
AQ=2t
AE=AQ·cos∠OAB=4t×
∴OE=OA-AE=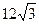 -
-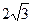 t
t
∴Q点的坐标为(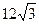 -
-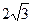 t,2t)
t,2t)
S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ
=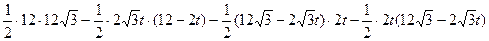
=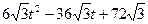
=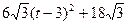 (
(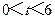 )
)
当t=3时,S△PQR最小=
(4)分三种情况:如图11.
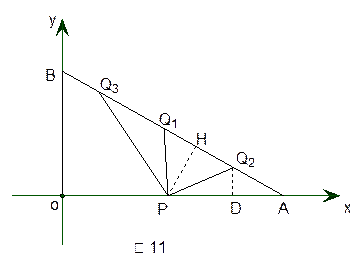
1当AP=AQ1=4t时,
∵OP+AP=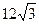
∴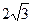 t+4t=
t+4t=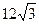
∴t=
或化简为t=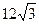 -18
-18
2当PQ2=AQ2=4t时
过Q2点作Q2D⊥x轴于点D,
∴PA="2AD=2A" Q2·cosA=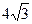 t
t
即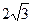 t+
t+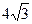 t =
t =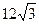
∴t=2
3当PA=PQ3时,过点P作PH⊥AB于点H
AH=PA·cos30°=( -
-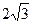 t)·
t)·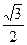 =18-3t
=18-3t
AQ3=2AH=36-6t
得36-6t=4t,
∴t=3.6
综上所述,当t=2,t=3.6,t=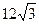 -18时,△APQ是等腰三角形.
-18时,△APQ是等腰三角形.
tan∠OAB=

∴∠OAB=30°
(2)如图10,连接O‘P,O‘M. 当PM与⊙O‘相切时,有∠PM O‘=∠PO O‘=90°,
△PM O‘≌△PO O‘

由(1)知∠OBA=60°
∵O‘M= O‘B
∴△O‘BM是等边三角形
∴∠B O‘M=60°可得∠O O‘P=∠M O‘P=60°
∴OP=" O" O‘·tan∠O O‘P =6×tan60°=
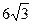
又∵OP=
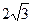 t
t∴
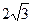 t=
t=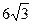 ,t=3
,t=3即:t=3时,PM与⊙O‘相切.
(3)如图9,过点Q作QE⊥x于点E
∵∠BAO=30°,AQ=4t
∴QE=
 AQ=2t
AQ=2tAE=AQ·cos∠OAB=4t×

∴OE=OA-AE=
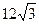 -
-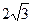 t
t∴Q点的坐标为(
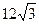 -
-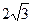 t,2t)
t,2t)S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ
=
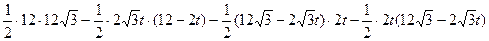
=
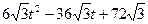
=
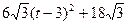 (
(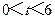 )
)当t=3时,S△PQR最小=

(4)分三种情况:如图11.

1当AP=AQ1=4t时,
∵OP+AP=
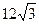
∴
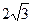 t+4t=
t+4t=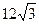
∴t=

或化简为t=
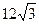 -18
-182当PQ2=AQ2=4t时
过Q2点作Q2D⊥x轴于点D,
∴PA="2AD=2A" Q2·cosA=
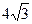 t
t即
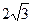 t+
t+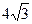 t =
t =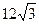
∴t=2
3当PA=PQ3时,过点P作PH⊥AB于点H
AH=PA·cos30°=(
 -
-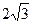 t)·
t)·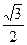 =18-3t
=18-3tAQ3=2AH=36-6t
得36-6t=4t,
∴t=3.6
综上所述,当t=2,t=3.6,t=
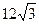 -18时,△APQ是等腰三角形.
-18时,△APQ是等腰三角形.
练习册系列答案
相关题目



 点出发,要到距离
点出发,要到距离
 的
的 地去,先沿北偏东
地去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了

 方向上
方向上 方向上
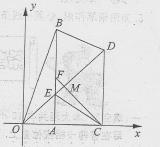
方向上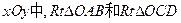 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,