题目内容
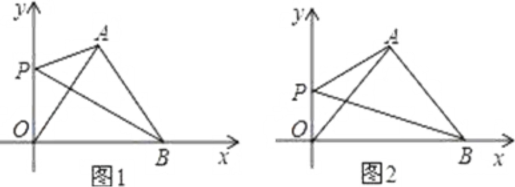
【题目】如图1,![]() 是
是![]() 的垂直平分线上一点,
的垂直平分线上一点,![]() 是
是![]() 轴上一点且
轴上一点且![]() .
.
(1)若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)在(1)的条件下,求证:![]() ;
;
(3)如图2,已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)(0,2);(2)见解析(3)10.
【解析】
(1)根据垂直平分线性质可得OA=AB,根据∠AOB的大小可以求得∠OPB=60°,根据30°角所对直角边为斜边一半即可求得P点坐标;
(2)在PB上取一点E,使OP=OE,可证∠POA=∠EOB,可证△POA≌△EOB,可得PA=EB,即可解题;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,可证BP=PD,即可求得PO+PB=OP+PD=OD即可解题.
解:(1)∵∠OPB=∠OAB,∠AOB=60°,
∴∠OPB=60°,
∴∠OBP=30°,
∵PB=4,
∴OP=2,
∴P点坐标为(0,2);
(2)在PB上取一点E,使OP=OE,

∵∠OPE=60°,
∴△POE是等边三角形,
∴∠POE=60°,PE=PO=OE,
∵∠AOB=60°,
∴∠POA=∠EOB
在△POA和△EOB中,
 ,
,
∴△POA≌△EOB(SAS),
∴PA=EB,
∴PB=PE+EB=PO+PA;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;

∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=5,
∴PO+PB=PO+PD=OD=2OE=10.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目