题目内容
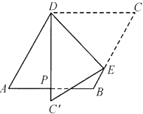
【题目】如图，菱形纸片
中，
，点
是
边的中点，折叠纸片，使点
落在直线
上的
处，折痕为经过点
的线段
．则
的度数为________．
【答案】75°
【解析】
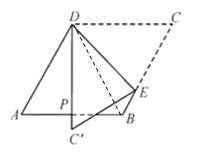
连接BD,可知△ABD是等边三角形，根据三线合一的性质得出DP平分∠ADB，即∠ADP=30°，再根据折叠性质可知，∠PDE=∠CDE=75°，然后根据三角形的内角和定理求出答案．
解：连接BD，
∵菱形
中，
，
∴AD=AB，AB∥CD
∴△ABD是等边三角形，∠ADC=120°
∵PA=PB
∴∠ADP=∠BDP=30°
根据折叠的性质可知：∠PDE=∠CDE
∴∠CDE=(∠ADC-∠ADP) ÷2=(120°-30°)÷2=45°
∵∠CDE+∠C+
=180°
∴=180°-(∠CDE+∠C)=180°-(45°+60°)=75°
故答案为：75°
练习册系列答案
相关题目
【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的，他把这根弹簧的上端固定，在其下端悬挂物体．下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值．
所挂质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 30 | 32 | 34 | 36 | 38 | 40 |
(1)上表所反映的变化过程中的两个变量，________是自变量，________是因变量；
(2)直接写y与x的关系式；
(3)当弹簧长度为130cm(在弹簧承受范围内)时，求所挂重物的质量．
