题目内容
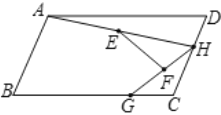
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点.连接
上的动点.连接![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .则
.则![]() 的最大值与最小值的差为( )
的最大值与最小值的差为( )
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
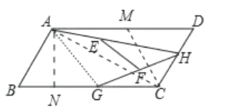
如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.首先证明∠ACD=90°,求出AC,AN,利用三角形中位线定理,可知EF=![]() AG,求出AG的最大值以及最小值即可解决问题.
AG,求出AG的最大值以及最小值即可解决问题.
解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,![]()
∴∠D=180°∠BCD=60°,AB=CD=4,
∵AM=DM=DC=4,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,AM=MC,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=![]()
在Rt△ACN中,∵AC=![]() ,∠ACN=∠DAC=30°,
,∠ACN=∠DAC=30°,
∴AN=![]() AC=
AC=![]()
∵AE=EH,GF=FH,
∴EF=![]() AG,
AG,
∵点G在BC上,∴AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为![]() ,最小值为
,最小值为![]() ,
,
∴EF的最大值为![]() ,最小值为
,最小值为![]() ,
,
∴EF的最大值与最小值的差为:![]()
故选:C

 阅读快车系列答案
阅读快车系列答案【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分(单位:分) | 中位数(单位:分) | 众数(单位:分) |
甲 | 74.2 |
| 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.