Question

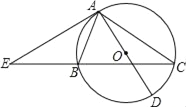
【题目】如图，△ABC内接于⊙O，AD是⊙O直径，过点A的切线与CB的延长线交于点E．

（1）求证：EA2=EBEC；

（2）若EA=AC，cos∠EAB=，AE=12，求⊙O的半径．

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）由弦切角定理，可得 继而可证得 然后由相似三角形的对应边成比例，证得
（2）首先连接过点B作BH⊥AE于点H，易证得 然后由三角函数的性质，求得直径的长，继而求得的半径．

试题解析：(1)证明：∵AE是切线，

∴∠EAB=∠C，

∵∠E是公共角，

∴△BAE∽△ACE，

∴EA:EC=EB:EA，

(2)连接BD，过点B作BH⊥AE于点H，

∵EA=AC，

∴∠E=∠C，

∵∠EAB=∠C，

∴∠EAB=∠E，

∴AB=EB，

∴在中,

∵AD是直径，

，

∴的半径为