题目内容
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )

A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
【答案】B
【解析】
依据直线y=kx+5+2k即可得到直线y=kx+5+2k(k≠0)经过定点P(-2,5),再根据直线PD的解析式为![]() ,直线PB的解析式为y=-2x+1,直线y=kx+5+2k(k≠0)与菱形ABCD有交点,即可得到k的取值范围.
,直线PB的解析式为y=-2x+1,直线y=kx+5+2k(k≠0)与菱形ABCD有交点,即可得到k的取值范围.
如图,
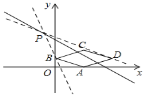
在直线y=kx+5+2k(k≠0)中,令x=﹣2,则y=5,
∴直线y=kx+5+2k(k≠0)经过定点P(﹣2,5),
由菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),
可得C(2,2),D(4,1),
∴易得直线PD的解析式为![]() ,直线PB的解析式为y=﹣2x+1,
,直线PB的解析式为y=﹣2x+1,
∵直线y=kx+5+2k(k≠0)与菱形ABCD有交点,
∴k的取值范围是![]() ,
,
故选B.

练习册系列答案
相关题目