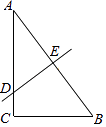题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,AD为△ABC角平分线. 
(1)用圆规在AB上作一点P,满足DP⊥AB;
(2)求:CD的长度.
【答案】
(1)解:)、如图,点P即为所求;

(2)解:∵AD平分∠BAC,
∴∠CAD=∠BAD.
又∵DC⊥AC、DP⊥AB,
∴∠C=∠APD.
在△ACD与APD中,
∵ 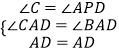 ,
,
∴△ACD≌APD(AAS).
∴AP=AC=4,CD=PD.
在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=5.
设DP为x,则DP=x,BD=3﹣x,在Rt△DPB中,∠DPB=90°,
∴DP2+PB2=DB2,即,x2+12=(3﹣x)2,
解得x= ![]() ,
,
∴CD=DP= ![]() .
.
【解析】(1)过点D作AB的垂线,垂足为P即可;(2)根据角平分线的性质可知∠CAD=∠BAD,利用AAS定理可知△ACD≌APD.在在Rt△ABC中根据勾股定理得出AB的长,设DP为x,则DP=x,BD=3﹣x,在Rt△DPB中,利用勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
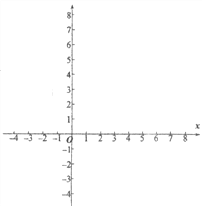
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①_____________________________________________;
②____________________________________________。