题目内容
【题目】如图,已知![]() ,
, ![]() .
.

(1)用直尺和圆规作出一条过点![]() 的直线
的直线![]() ,使得点
,使得点![]() 关于直线
关于直线![]() 的对称点落在边
的对称点落在边![]() 上(不写作法,保留作图痕迹).
上(不写作法,保留作图痕迹).
(2)设直线![]() 与边
与边![]() 的交点为
的交点为![]() ,且
,且![]() ,请你通过观察或测量,猜想线段
,请你通过观察或测量,猜想线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)作图见解析.( 2 ) ![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)先作∠BAC的平分线l,再过点C作CF⊥l交AB于F,则可得到点C和F点关于l对称,所以l为所作;
(2)连结DF,如图,利用等腰三角形的判定方法得到AF=AC,则AD垂直平分CF,所以DF=DC,则∠DCF=∠DFC,再利用三角形外角性质得∠BDF=2∠DCF,接着证明∠B=2∠BCF,于是得到∠B=∠BDF,则FB=FD=CD,则易得AB=AF+FB=AC+CD.
试题解析:(1)如图,直线l为所作;
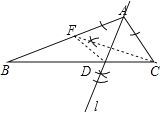
(2)AB=AC+CD.理由如下:
连结DF,如图,
∵AD平分∠BAC,AD⊥CF,
∴AF=AC,
∴AD垂直平分CF,
∴DF=DC,
∴∠DCF=∠DFC,
∴∠BDF=∠DCF+∠DFC=2∠DCF,
∵∠AFC=∠ACF,
∵∠AFC=∠B+∠BCF,
∴∠ACF=∠B+∠BCF,
∵∠ACB=2∠B,
∴2∠B-∠BCF=∠B+∠BCF,
∴∠B=2∠BCF,
∴∠B=∠BDF,
∴FB=FD,
∴FB=CD,
∴AB=AF+FB=AC+CD.

练习册系列答案
相关题目



