Question

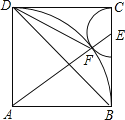
【题目】如图，在正方形ABCD中，E是BC边上的一点，以E为圆心，EC为半径的半圆与以A为圆心AB为半径的圆弧相外切于点F，若AB＝4，

(1)求半圆E的半径r的长；

(2)求四边形ADCE的面积；

(3)连接DB、DF，设∠BDF＝α，∠AEC＝β，求证：β－2α＝90°．

Answer 1

【答案】(1)1；(2)10；(3)证明见解析．

【解析】分析：

（1）根据正方形的性质求出AB、AE、BE的长，在Rt△ABE中根据勾股定理得出方程，求出方程的解即可；

（2）根据梯形的面积公式求出即可；

（3）根据三角形的外角性质求出β=∠BAE+90°，根据圆周角定理得出∠BDF=∠BAE，代入求出即可．

本题解析：

(1)在Rt△ABE中，AB=BC=AF=AD=DC=4，

BE=BCCE=4r，AE=BF+EF=4+r，

∵AE=AB+BE，

∴(4+r)=4+(4r)，

解得：r=1，

答：半E的半径r的长是1.

(2)梯形ADCE的面积是S=DC(AD+CE)= ×4×(4+1)=10，

答：四边形ADCE的面积是10.

(3)证明：∵∠AEC是Rt△ABE的外角,

∴β=∠BAE+90°，

∵∠BDF=∠BAE，

∴α=∠BAE，

即∠BAE=2α，

∴β=2α+90°，

即β2α=90°.