题目内容
【题目】已知：在平面直角坐标系中有两条直线y=﹣2x+3和y=3x﹣2．
(1)确定这两条直线交点所在的象限，并说明理由；
(2)求两直线与坐标轴正半轴围成的四边形的面积．
【答案】(1)两直线交点坐标为(1，1)，在第一象限；(2)
.
【解析】
(1)联立两直线解析式成方程组，解方程组即可求出交点坐标，进而即可得出交点所在的象限；
(2)令直线y=﹣2x+3与x、y轴分别交于点A、B，直线y=3x﹣2与x、y轴分别交于点C、D，两直线交点为E，由直线AB、CD的解析式即可求出点A、B、C的坐标，利用分割图形求面积法结合三角形的面积公式即可求出两直线与坐标轴正半轴围成的四边形的面积．
(1)联立两直线解析式得：
，
解得：
，
∴两直线交点坐标为(1，1)，在第一象限．
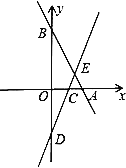
(2)令直线y=﹣2x+3与x、y轴分别交于点A、B，直线y=3x﹣2与x、y轴分别交于点C、D，两直线交点为E，如图所示．
令y=﹣2x+3中x=0，则y=3，
∴B(0，3)；
令y=﹣2x+3中y=0，则x=
，
∴A(，0)．
令y=3x﹣2中y=0，则x=
，
∴C(，0)．
∵E(1，1)，
∴S四边形OCEB=S△AOB﹣S△ACE=
OAOB﹣ACyE=××3﹣×(﹣)×1=．
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润=收入﹣成本），并指出售价为多少元时获得最大利润，最大利润是多少？
