题目内容
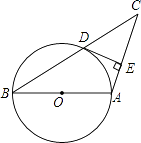
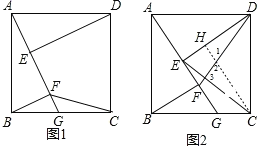
【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
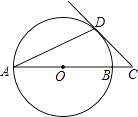
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


【答案】(1)![]() ;(2)DF=CE,DF⊥CE.理由见解析;
;(2)DF=CE,DF⊥CE.理由见解析;
【解析】(1)如图1,先利用勾股定理计算出AG=![]() =5,再利用面积法和勾股定理计算出
=5,再利用面积法和勾股定理计算出![]() 然后证明△ABF≌△DAE,得到DE=AF=
然后证明△ABF≌△DAE,得到DE=AF=![]() ;
;
(2)作CH⊥DE于H,如图2,先利用△ABF≌△DAE,得到![]() 则
则![]() 与(1)的证明方法一样可得△CDH≌△DAE,则
与(1)的证明方法一样可得△CDH≌△DAE,则![]()
![]() 于是可判断EH=EF,接着证明△DEF≌△CHE,所以DF=CE,∠EDF=∠HCE,然后利用三角形内角和得到
于是可判断EH=EF,接着证明△DEF≌△CHE,所以DF=CE,∠EDF=∠HCE,然后利用三角形内角和得到![]() 从而判断DF⊥CE.
从而判断DF⊥CE.
(1)如图1,
∵四边形ABCD是正方形,
∴![]() ,
,
∵DE⊥AG,BF⊥AG,
∴![]()
在Rt△ABG中,AG=![]() =5,
=5,
∵![]()
∴![]()
∴AF=![]() =
=![]() =
=![]() ,
,
∵![]()
∴∠ABF=∠DAE,
在△ABF和△DAE中
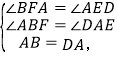
∴△ABF≌△DAE,
∴DE=AF=![]() ;
;
(2)DF=CE,DF⊥CE.理由如下:
作CH⊥DE于H,如图2,
∵△ABF≌△DAE,
∴![]()
∴![]()
与(1)的证明方法一样可得△CDH≌△DAE,
∴![]()
∴![]()
∴EH=EF,
在△DEF和△CHE中
∴△DEF≌△CHE,
∴DF=CE,∠EDF=∠HCE,
∵∠1=∠2,
∴![]()
∴DF⊥CE.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某中学八年级的篮球队有![]() 名队员.在罚篮投球训练中,这
名队员.在罚篮投球训练中,这![]() 名队员各投篮
名队员各投篮![]() 次的进球情况如下表:
次的进球情况如下表:
进球数 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
针对这次训练,请解答下列问题:
![]() 这
这![]() 名队员进球数的平均数是________,中位数是________;
名队员进球数的平均数是________,中位数是________;
![]() 求这支球队罚篮命中率.罚篮命中率
求这支球队罚篮命中率.罚篮命中率![]() (进球数
(进球数![]() 投篮次数)
投篮次数)![]() ________;
________;
![]() 若队员小亮的罚篮命中率为
若队员小亮的罚篮命中率为![]() ,请你分析小亮在这支球队中的罚篮水平.
,请你分析小亮在这支球队中的罚篮水平.