题目内容
【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.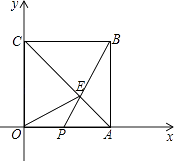
(1)求点E的坐标:
(2)求△OPE的周长.
【答案】
(1)解:过点E作EM⊥y轴于点M,
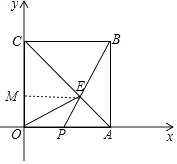
则 ![]() OCEM=12,
OCEM=12,
即 ![]() ×6×EM=12,
×6×EM=12,
∴EM=4,
∵四边形OABC是正方形,
∴∠MCE=45°,
∴△MEC是等腰直角三角形,
∴MC=ME=4,
∴MO=6﹣4=2,
∴点E的坐标是(4,2);
(2)解:设直线BE的解析式为y=kx+b,
把B(6,6)和点E(4,2)的坐标代入函数解析式得: ![]()
解得:k=2,b=﹣6,
∴直线BE的解析式为y=2x﹣6,
令2x﹣6=0得:x=3,
∴点P的坐标为(3,0),
∴OP=3,
∵四边形ABCO是正方形,
∴OC=CB,∠BCE=∠OCE,
在△OCE和△BCE中
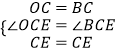
∴△OCE≌△BCE(SAS),
∴OE=BE,
在Rt△PBA中,由勾股定理可得:PB= ![]() =3
=3 ![]() ,
,
∴△OPE的周长=OE+PE+OP=3+PB=3+3 ![]() .
.
【解析】(1)题中已知△OCE的面积为12.因此过点E作EM⊥y轴于点M,利用三角形面积公式可求出ME的长,再证明△CME是等腰直角三角形,就可求出OM的长,即可求出点E的坐标。
(2)根据已知求出点B的坐标,利用待定系数法求出直线BE的解析式,再求出点P的坐标,即可求出OP的长,再证明△OCE≌△BCE,得到OE=BE,因此△OPE的周长就等于OP+BP,利用勾股定理求出PB的长,即可求得此三角形的周长。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()