Question

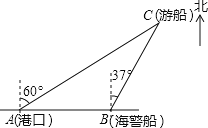
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，

（1）求点C到直线AB的距离；

（2）求海警船到达事故船C处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）

Answer 1

【答案】(1)40 (2)

【解析】试题分析：（1）过点C作CD⊥AB，交AB的延长线于点D．在Rt△ACD中，求出CD的长即可；

（2）海警船到达事故船C的距离为50海里，除以40海里/小时即可解答．

试题解析：（1）如图，过点C作CD⊥AB交AB延长线于D．

在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，

∴点C到直线AB距离CD=AC=40．

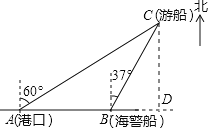
（2）在Rt△CBD中，∵∠CDB=90°，∠CBD=90°﹣37°=53°，

∴BC==50（海里），

∴海警船到达事故船C处所需的时间大约为：50÷40= (小时）．