题目内容
【题目】已知：如图，在□ABCD中，MN∥AC ， 分别交DA ， DC的延长线于点M ， N ， 交AB ， BC于点P ， Q.求证：MP＝NQ ．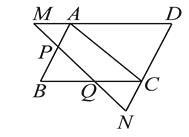 
【答案】证明：∵四边形ABCD为平行四边形，
∴AP∥CN
又∵MN∥AC ，
∴ 四边形ACNP为平行四边形，
∴ MQ＝AC＝NP ．
∴ MQ－PQ＝NP－PQ ，
即MP＝NQ ．
【解析】本题主要考查了平行四边形的判定与性质，由已知□ABCD和MN∥AC ， 推出AP∥CN ， MN∥AC从而得到图中平行四边形．
【考点精析】本题主要考查了平行四边形的判定的相关知识点，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
