题目内容
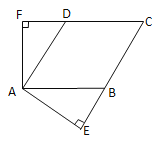
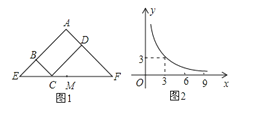
【题目】图(1)所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
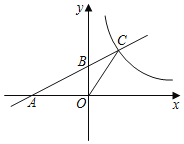
与![]() 满足的反比例函数关系如图(2)所示,等腰直角三角形
满足的反比例函数关系如图(2)所示,等腰直角三角形![]() 的斜边
的斜边![]() 过点
过点![]() ,
,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A. 当![]() 时,
时,![]()
B. 当![]() 时,
时,![]()
C. 当![]() 增大时,
增大时,![]() 的值增大
的值增大
D. 当![]() 增大时,
增大时,![]() 的值不变
的值不变
【答案】D
【解析】
由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图像得出反比例函数解析式为y=![]() ;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3
;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3![]() ,CF=3
,CF=3![]() ,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10
,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10![]() ,而EM=5
,而EM=5![]() ;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值;由于ECCF=
;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值;由于ECCF=![]() x×
x×![]() y=2xy,其值为定值.
y=2xy,其值为定值.
解:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;观察反比例函数图像得x=3,y=3,则反比例解析式为y=![]() .
.
A、当x=3时,y=3,即BC=CD=3,所以CE=![]() BC=3
BC=3![]() ,CF=
,CF=![]() CD=3
CD=3![]() ,C点与M点重合,则EC=EM,所以A选项错误;
,C点与M点重合,则EC=EM,所以A选项错误;
B、当y=9时,x=1,即BC=1,CD=9,所以EC=![]() ,EF=10
,EF=10![]() ,EM=5
,EM=5![]() ,所以B选项错误;
,所以B选项错误;
C、因为ECCF=![]() x
x![]() y=2×xy=18,所以,ECCF为定值,所以C选项错误;
y=2×xy=18,所以,ECCF为定值,所以C选项错误;
D、因为BEDF=BCCD=xy=9,即BEDF的值不变,所以D选项正确.
故选:D.

练习册系列答案
相关题目