ЬтФПФкШн
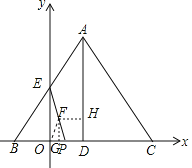
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ AB=AC=10ЃЌЯпЖЮBCдк![]() жсЩЯЃЌBC=12ЃЌЕуBЕФзјБъЮЊЃЈЃ3ЃЌ0ЃЉЃЌЯпЖЮABНЛ
жсЩЯЃЌBC=12ЃЌЕуBЕФзјБъЮЊЃЈЃ3ЃЌ0ЃЉЃЌЯпЖЮABНЛ![]() жсгкЕуEЃЌЙ§AзїADЁЭBCгкDЃЌЖЏЕуPДгдЕуГіЗЂЃЌвдУПУы3ИіЕЅЮЛЕФЫйЖШби
жсгкЕуEЃЌЙ§AзїADЁЭBCгкDЃЌЖЏЕуPДгдЕуГіЗЂЃЌвдУПУы3ИіЕЅЮЛЕФЫйЖШби![]() жсЯђгвдЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊ
жсЯђгвдЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊ![]() УыЃЎ
УыЃЎ
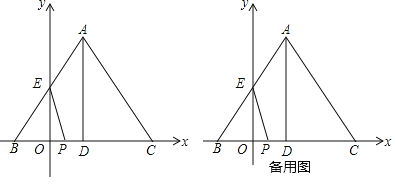
ЃЈ1ЃЉЕБЁїBPEЪЧЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєЕуPдЫЖЏЕФЭЌЪБЃЌЁїABCвдBЮЊЮЛЫЦжааФЯђгвЗХДѓЃЌЧвЕуCЯђгвдЫЖЏЕФЫйЖШЮЊУПУы2ИіЕЅЮЛЃЌЁїABCЗХДѓЕФЭЌЪБИпADвВЫцжЎЗХДѓЃЌЕБвдEPЮЊжБОЖЕФдВгыЖЏЯпЖЮADЫљдкжБЯпЯрЧаЪБЃЌЧѓ![]() ЕФжЕКЭДЫЪБЕуCЕФзјБъЃЎ
ЕФжЕКЭДЫЪБЕуCЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉt=![]() Лђt=1Лђt=
Лђt=1Лђt=![]() ЃЛЃЈ2ЃЉЕБt=1ЪБЁбFгыЖЏЯпЖЮADЫљдкжБЯпЯрЧаЃЌДЫЪБCЃЈ11ЃЌ0ЃЉЃЎ
ЃЛЃЈ2ЃЉЕБt=1ЪБЁбFгыЖЏЯпЖЮADЫљдкжБЯпЯрЧаЃЌДЫЪБCЃЈ11ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШЧѓГіжБЯпABЕФНтЮіЪНЃЌНјЖјЗжБ№РћгУЂйЕБBEЃНBPЪБЃЌЂкЕБEBЃНEPЪБЃЌЂлЕБPBЃНPEЪБЃЌЕУГіtЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЪзЯШЕУГіЁїPGFЁзЁїPOEЃЌдйРћгУдкRtЁїEOPжаЃКEP2ЃНOP2ЃЋEO2ЃЌНјЖјЧѓГіtЕФжЕвдМАCЕузјБъЃЎ
ЃЈ1ЃЉЁпAB=ACЃЌADЁЭBCЃЌ
ЁрBD=CD=6ЃЌ
ЁпAB=10ЃЌЁрAD=8ЃЌЁрAЃЈ3ЃЌ8ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЌдђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊЃКy=![]() x+4ЃЌ
x+4ЃЌ
ЁрEЃЈ0ЃЌ4ЃЉЃЌ
ЁрBE=5ЃЌ
ЕБЁїBPEЪЧЕШбќШ§НЧаЮгаШ§жжЧщПіЃК
ЂйЕБBE=BPЪБЃЌ3+3t=5ЃЌНтЕУЃКt=![]() ЃЛ
ЃЛ
ЂкЕБEB=EPЪБЃЌ3t=3ЃЌНтЕУЃКt=1ЃЛ
ЂлЕБPB=PEЪБЃЌ
ЁпPB=PEЃЌAB=ACЃЌЁЯABC=ЁЯPBEЃЌ
ЁрЁЯPEB=ЁЯACB=ЁЯABCЃЌ
ЁрЁїPBEЁзЁїABCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУЃКt=
ЃЌНтЕУЃКt=![]() ЃЌ
ЃЌ
злЩЯЃКt=![]() Лђt=1Лђt=
Лђt=1Лђt=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃКCЃЈ9+2tЃЌ0ЃЉЃЌ
ЁрBC=12+2tЃЌBD=CD=6+tЃЌOD=3+tЃЌ
ЩшFЮЊEPЕФжаЕуЃЌСЌНгOFЃЌзїFHЁЭADЃЌFGЁЭOPЃЌ
ЁпFGЁЮEOЃЌ
ЁрЁїPGFЁзЁїPOEЃЌ
ЁрPG=OG=![]() tЃЌFG=
tЃЌFG=![]() EO=2ЃЌЁрFЃЈ
EO=2ЃЌЁрFЃЈ![]() tЃЌ2ЃЉЃЌ
tЃЌ2ЃЉЃЌ
ЁрFH=GD=ODЉOG=3+tЉ![]() t=3Љ
t=3Љ![]() tЃЌ
tЃЌ
ЁпЁбFгыЖЏЯпЖЮADЫљдкжБЯпЯрЧаЃЌFH=![]() EP=3Љ
EP=3Љ![]() tЃЌ
tЃЌ
дкRtЁїEOPжаЃКEP2=OP2+EO2
Ёр4ЃЈ3Љ![]() tЃЉ2=ЃЈ3tЃЉ2+16
tЃЉ2=ЃЈ3tЃЉ2+16
НтЕУЃКt1=1ЃЌt2=Љ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕБt=1ЪБЁбFгыЖЏЯпЖЮADЫљдкжБЯпЯрЧаЃЌДЫЪБCЃЈ11ЃЌ0ЃЉЃЎ