题目内容
【题目】如图,在矩形OABC中,点A,B的坐标分别为A(4,0),B(4,3),动点N,P分别从点B,A同时出发,点N以1单位/秒的速度向终点C运动,点P以5/4单位/秒的速度向终点C运动,连结NP,设运动时间为t秒(0<t<4)
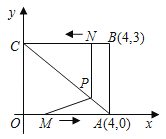
(1)直接写出OA,AB,AC的长度;
(2)求证:△CPN∽△CAB;
(3)在两点的运动过程中,若点M同时以1单位/秒的速度从点O向终点A运动,求△MPN的面积S与运动的时间t的函数关系式(三角形的面积不能为0),并直接写出当S=![]() 时,运动时间t的值.
时,运动时间t的值.
【答案】(1)OA=4,AB=3,AC=5;(2)见解析;(3)t的值为(3﹣![]() )秒
)秒
【解析】
(1)由矩形的性质和已知条件得出OA=BC=4,AB=OC=3,∠AOC=90°,由勾股定理求出AC=![]() =5;
=5;
(2)由题意得BN=t,AP=![]() t,证出
t,证出![]() =
=![]() ,得出PN∥AB,即可得出△CPN∽△CAB;
,得出PN∥AB,即可得出△CPN∽△CAB;
(3)①当0<t<2时,延长NP交OA于D,由相似三角形的性质得![]() =
=![]() =
=![]() ,求出PD=
,求出PD=![]() t,AD=t,得出PN=3﹣
t,AD=t,得出PN=3﹣![]() t,DM=4﹣2t,由三角形面积公式即可得出答案;
t,DM=4﹣2t,由三角形面积公式即可得出答案;
②2<t<4时,延长NP交OA于D,由相似三角形的性质得出![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,求出PD=
,求出PD=![]() t,AD=t,得出PN=3﹣
t,AD=t,得出PN=3﹣![]() t,DM=2t﹣4,由三角形面积公式即可得出答案;再把S=
t,DM=2t﹣4,由三角形面积公式即可得出答案;再把S=![]() 分别代入两个关系式,解方程即可.
分别代入两个关系式,解方程即可.
(1)证明:∵四边形OABC是矩形,A(4,0),B(4,3),
∴OA=BC=4,AB=OC=3,∠AOC=90°,
∴AC=![]() =
=![]() =5;
=5;
(2)解:由题意得:BN=t,AP=![]() t,
t,
∵![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PN∥AB,
∴△CPN∽△CAB;
(3)解:分两种情况:
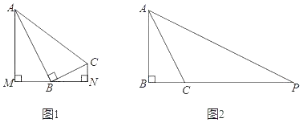
①当0<t<2时,延长NP交OA于D,如图1所示:
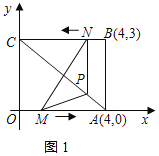
由(2)得:PD∥AB,
∴△APD∽△ACO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:PD=![]() t,AD=t,
t,AD=t,
∴PN=3﹣![]() t,DM=4﹣t﹣t=4﹣2t,
t,DM=4﹣t﹣t=4﹣2t,
∴△MPN的面积S=![]() PN×DM=
PN×DM=![]() ×(3﹣
×(3﹣![]() t)×(4﹣2t)=
t)×(4﹣2t)=![]() t2﹣
t2﹣![]() t+6,
t+6,
即S=![]() t2﹣
t2﹣![]() t+6(0<t<2);
t+6(0<t<2);
②当2<t<4时,延长NP交OA于D,如图2所示:
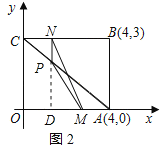
由(2)得:PD∥AB,
∴△APD∽△ACO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:PD=![]() t,AD=t,
t,AD=t,
∴PN=3﹣![]() t,DM=t+﹣4t=2t﹣4,
t,DM=t+﹣4t=2t﹣4,
∴△MPN的面积S=![]() PN×DM=
PN×DM=![]() ×(3﹣
×(3﹣![]() t)×(2t﹣4)=﹣
t)×(2t﹣4)=﹣![]() t2+
t2+![]() t﹣6,
t﹣6,
即S=﹣![]() t2+
t2+![]() t﹣6(2<t<4);
t﹣6(2<t<4);
当S=![]() ,0<t<2时,则
,0<t<2时,则![]() t2﹣
t2﹣![]() t+6=
t+6=![]() ,
,
整理得:t2﹣6t+6=0,
解得:t=3﹣![]() ,或t=3+
,或t=3+![]() (不合题意舍去),
(不合题意舍去),
∴t=3﹣![]() ;
;
当S=![]() ,2<t<4时,则﹣
,2<t<4时,则﹣![]() t2+
t2+![]() t﹣6=
t﹣6=![]() ,
,
整理得:t2﹣6t+10=0,
∵△=36﹣40<0,
∴此方程无解;
综上所述,当S=![]() 时,运动时间t的值为(3﹣
时,运动时间t的值为(3﹣![]() )秒.
)秒.