题目内容
【题目】在∠ABC中,∠ABC=90°,tan∠BAC=![]() .
.
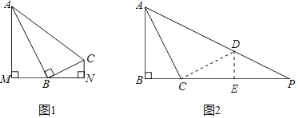
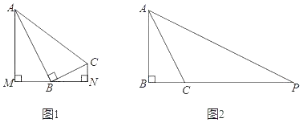
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,若点B恰好是线段MN的中点,求tan∠BAM的值;
(2)如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
【答案】(1)tan∠BAM=![]() ;(2)tan∠PAC=
;(2)tan∠PAC=![]() .
.
【解析】
(1)先证明∠M=∠N=90°,∠MAB=∠NBC,那么△AMB∽△BNC,根据相似三角形对应边成比例得出![]() =tan∠BAC=
=tan∠BAC=![]() .由线段中点的定义可得BM=BN,然后在Rt△AMB中,利用正切函数的定义即可求出tan∠BAM的值;
.由线段中点的定义可得BM=BN,然后在Rt△AMB中,利用正切函数的定义即可求出tan∠BAM的值;
(2)过点C作CD⊥AC交AP于点D,过点D作DE⊥BP于点E.根据正切函数的定义得出tan∠BAC=![]() ,tan∠APB=
,tan∠APB=![]() .而∠APB=∠BAC,那么可设BC=x,则AB=2x,得出BP=4x,则CP=3x.同理(1)中,易证∠BAC=∠ECD,根据等腰三角形的判定与性质得出CE=EP=
.而∠APB=∠BAC,那么可设BC=x,则AB=2x,得出BP=4x,则CP=3x.同理(1)中,易证∠BAC=∠ECD,根据等腰三角形的判定与性质得出CE=EP=![]() CP=
CP=![]() x.再证明△ABC∽△CED,根据相似三角形对应边成比例得出
x.再证明△ABC∽△CED,根据相似三角形对应边成比例得出![]() ,然后在Rt△ACD中,利用正切函数的定义即可求出tan∠PAC的值.
,然后在Rt△ACD中,利用正切函数的定义即可求出tan∠PAC的值.
(1)如图 1.
∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°,
∴∠MAB+∠ABM=90°,
∵∠ABC=90°,
∴∠NBC+∠ABM=90°,
∴∠MAB=∠NBC,
∴△AMB∽△BNC,
∴![]() =tan∠BAC=
=tan∠BAC=![]() .
.
∵点B是线段MN的中点
∴BM=BN,
∴在Rt△AMB中,tan∠BAM=![]() ;
;
(2)如图2,过点C作CD⊥AC交AP于点D,过点D作DE⊥BP于点E.
∵tan∠BAC=![]() ,∠APB=∠BAC,
,∠APB=∠BAC,
∴tan∠BAC=![]() ,tan∠APB=
,tan∠APB=![]() .
.
设BC=x,则AB=2x,BP=4x,则CP=BP﹣BC=4x﹣x=3x.
同理(1)中,可得∠BAC=∠ECD,
∴∠APB=∠ECD.
∵DE⊥BP,
∴CE=EP=![]() CP=
CP=![]() x.
x.
同理(1)中,可得△ABC∽△CED,
∴![]() ,
,
∴在Rt△ACD中,tan∠PAC=![]() .
.