题目内容
【题目】对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”n的各个数位上的数字之和记为F（n）．例如n=135时，F（135）=1+3+5=9．
（1）对于“相异数”n，若F（n）=6，请你写出一个n的值；
（2）若a，b都是“相异数”，其中a=100x+12，b=350+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k＝
，当F（a）+F（b）=18时，求k的最小值．
【答案】（1）123；（2）
.
【解析】
（1）由定义可得．
（2）根据题意先求出F（a）=x+3，F（b）=8+y，代入可得二元一次方程x+y=7，求出x，y的解代入可得k的值．
（1）∵F（n）=6
∴n=123
（2）∵F（a）=x+1+2=x+3，F（b）=3+5+y=8+y且F（a）+F（b）=18
∴x+3+8+y=18
∴x+y=7
∵x，y是正整数
∴
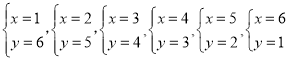
∵a，b是相异数，
∴a≠1，a≠2，b≠3，b≠5
∴
,
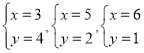∴k=
=或
或1
∴k的最小值为.（1）
，
；
练习册系列答案
相关题目
