题目内容
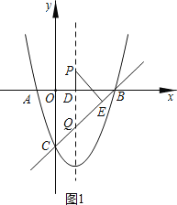
【题目】如图1,在平面直角坐标系中,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A(-1,0),点B,与y轴交于点C(0,-3),作直线BC.点P是抛物线的对称轴上的一个动点,P点到x轴和直线BC的距离分别为PD、PE.
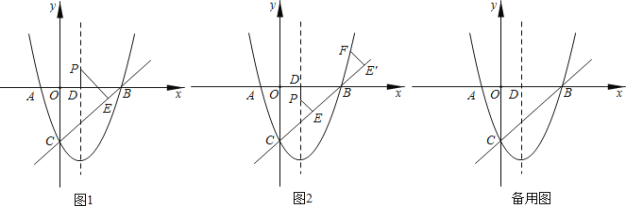
(1)求抛物线解析式;
(2)当P点运动过程中满足PE=PD时,求此时点P的坐标;
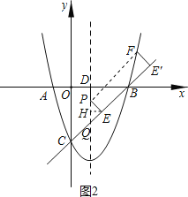
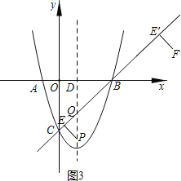
(3)如图2,从点B处沿着直线BC的垂线翻折PE得到FE',当点F在抛物线上时,求点P的坐标.
【答案】(1)y=x2-2x-3;(2)点P坐标为(1,2+2![]() )或(1,2-2
)或(1,2-2![]() );(3)点P坐标为(1,2+
);(3)点P坐标为(1,2+![]() )或(1,2-
)或(1,2-![]() ).
).
【解析】
(1)由点A、B关于对称轴:直线x=1对称,得B(3,0),再根据待定系数法,即可求解;
(2)易得直线BC解析式为:y=x-3,∠OCB=45°,从而得Q(1,-2),设P(1,t),则PD=|t|,PQ=|t+2|,结合PQ=![]() PD,即可求解;
PD,即可求解;
(3)分两种情况:①当点P(1,t)在点Q上方时,②当点P(1,t)在点Q下方时,分别进行求解即可.
(1)∵抛物线与x轴交于点A(-1,0)、点B,
∴点A、B关于对称轴:直线x=1对称,
∴![]() =1,解得:xB=3,
=1,解得:xB=3,
∴B(3,0)
∵抛物线y=ax2+bx+c经过点A、B、C(0,-3)
∴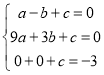 解得:
解得: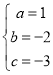 ,
,
∴抛物线解析式为y=x2-2x-3;
(2)如图1,记直线BC与对称轴交点为Q,
∵B(3,0),C(0,-3),
∴直线BC解析式为:y=x-3,∠OCB=45°,
∴Q(1,-2),
设P(1,t),则PD=|t|,PQ=|t+2|
∵PE⊥BC于点E,
∴∠PEQ=90°,
∵PQ∥y轴,
∴∠PQE=∠OCB=45°,
∴Rt△PEQ中,PQ=![]() PE
PE
∵PE=PD,
∴PQ=![]() PD,
PD,
∴PQ2=2PD2,
∴(t+2)2=2t2,
解得:t1=2+2![]() ,t2=2-2
,t2=2-2![]()
∴点P坐标为(1,2+2![]() )或(1,2-2
)或(1,2-2![]() );
);
(3)①如图2
连接PF,过点E作EH⊥PQ于点H,
∵∠PQE=45°,∠PEQ=90°,
∴△PEQ是等腰直角三角形,
∴PH=QH=EH=![]() PQ=
PQ=![]() ,
,
即点E向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位可得点P,
个单位可得点P,
∴xE=xP+![]() =
=![]() +2,yE=yP-
+2,yE=yP-![]() =
=![]() -1,即E(
-1,即E(![]() +2,
+2,![]() -1),
-1),
∵从点B处沿着直线BC的垂线翻折PE得到FE',
∴FE'⊥BC,FE'=PE,
∴FE'∥PE,
∴四边形PEE'F是平行四边形,
∴EE'∥PF,即EE'向左平移![]() 个单位、向上平移
个单位、向上平移![]() 个单位可得PF,
个单位可得PF,
∵点B为EE'中点,
∴![]() =xB=3,yE'=-yE=1-
=xB=3,yE'=-yE=1-![]() ,
,
∴xE'=4-![]() ,
,
∴xF=xE'-![]() =3-t,yF=yE'+
=3-t,yF=yE'+![]() =2,即F(3-t,2),
=2,即F(3-t,2),
∵点F在抛物线上,
∴(3-t)2-2(3-t)-3=2,
解得:t1=2+![]() ,t2=2-
,t2=2-![]() ,
,
②如图3,当点P(1,t)在点Q下方时,t<-2,
则翻折后点F在直线BC下方,不可能在抛物线上,
综上所述,点P坐标为(1,2+![]() )或(1,2-
)或(1,2-![]() ).
).

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】为了解居民用水情况,小明在某小区随机抽查了20户家庭的月用水量,结果如下表:
月用水量(m3) | 4 | 5 | 6 | 8 | 9 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法错误的是( )
A.中位数是6m![]() B.平均数是5.8m
B.平均数是5.8m![]()
C.众数是6m![]() D.极差是6m
D.极差是6m![]()
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?