Question

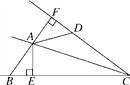
【题目】如图，AC平分∠BCD，AB＝AD，AE⊥BC于E，AF⊥CD于F.

(1)若∠ABE＝60°，求∠CDA的度数；

(2)若AE＝2，BE＝1，CD＝4.求四边形AECD的面积．

Answer 1

【答案】（1）120°；（2）9.

【解析】(1)、根据角平分线的性质以及AB=AD得出Rt△ABE和Rt△ADF全等，从而得出∠ADF＝∠ABE＝60°，根据平角得出∠ADC的度数；(2)、根据三角形全等得出FD＝BE＝1，AF＝AE＝2，CE＝CF＝CD＋FD＝5，最后根据S四边形AECD＝S△AEC＋S△ACD得出答案．

解：(1)∵AC平分∠BCD，AE⊥BC，AF⊥CD，

∴∠ACE＝∠ACF，∠AEC＝∠AFC＝90°，

∴AE＝AF， 在Rt△ABE和Rt△ADF中，AE=AF，AB=AD，∴Rt△ABE≌Rt△ADF(HL)，

∴∠ADF＝∠ABE＝60°， ∴∠CDA＝180°－∠ADF＝120°；

(2)由(1)知Rt△ABE≌Rt△ADF， ∴FD＝BE＝1，AF＝AE＝2，

在△AEC和△AFC中，∠ACE=∠ACF，∠AEC=∠AFC，AC=AC，∴△AEC≌△AFC(AAS)，

∴CE＝CF＝CD＋FD＝5，

∴S四边形AECD＝S△AEC＋S△ACD＝EC·AE＋CD·AF＝×5×2＋×4×2＝9．