题目内容
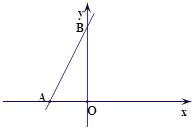
【题目】如图,已知一次函数y=﹣x+n的图象与反比例函数y=![]() 的图象交于A(4,﹣2),B(﹣2,m)两点.
的图象交于A(4,﹣2),B(﹣2,m)两点.
(1)请直接写出不等式﹣x+n≤![]() 的解集;
的解集;
(2)求反比例函数和一次函数的解析式;
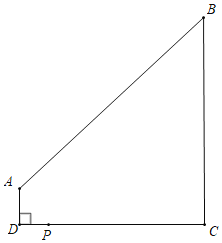
(3)过点A作x轴的垂线,垂足为C,连接BC,求△ABC的面积.
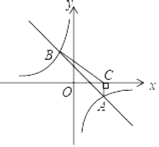
【答案】(1)﹣2≤x<0或x≥4;(2)y=﹣![]() ,y=﹣x+2;(3)6
,y=﹣x+2;(3)6
【解析】
(1)根据图像即可得到答案;
(2)将点A(4,﹣2),B(﹣2,m)的坐标分别代入解析式即可得到答案;
(3) 过点B作BD⊥AC,根据点A、B的坐标求得AC、BD的长度,即可求得图形面积.
解:(1)由图象可知:不等式﹣x+n≤![]() 的解集为﹣2≤x<0或x≥4;
的解集为﹣2≤x<0或x≥4;
(2)∵一次函数y=﹣x+n的图象与反比例函数y=![]() 的图象交于A(4,﹣2),B(﹣2,m)两点.
的图象交于A(4,﹣2),B(﹣2,m)两点.
∴k=4×(﹣2)=﹣2m,﹣2=﹣4+n
解得m=4,k=﹣8,n=2,
∴反比例函数和一次函数的解析式分别为y=﹣![]() ,y=﹣x+2;
,y=﹣x+2;
(3)由(2)知B(-2,4),
过点B作BD⊥AC,交AC的延长线于D,
∵A(4,﹣2),B(-2,4),
∴AC=2,BD=2+4=6,
S△ABC=![]() .
.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目