题目内容
【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(s,t)(s≠0). 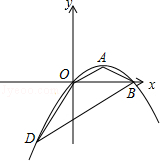
(1)当s=2时,t=1时,求抛物线对应的二次函数的表达式;
(2)若(1)中的抛物线与x轴交于点B,过B作OA的平行线交抛物线于点D,求△BDO三条高的和;
(3)当点A在抛物线y=x2﹣x上,且﹣1≤s<2时,求a的取值范围.
【答案】
(1)解:由题意可知A(2,1),
设抛物线的解析式为y=a(x﹣2)2+1,
由于抛物线过原点,
∴将(0,0)代入y=a(x﹣2)2+1,
∴解得a=﹣ ![]() ,
,
∴抛物线的解析式为:y=﹣ ![]() (x﹣2)2+1
(x﹣2)2+1
(2)解:令y=0代入y=﹣ ![]() (x﹣2)2+1,
(x﹣2)2+1,
∴解得x=4或x=0,
∴B(4,0)
设直线OA的解析式为:y=kx,
将A(2,1)代入y=kx,
∴k= ![]() ,
,
∵BD∥OA,
∴设直线BD的解析式为:y= ![]() x+m,
x+m,
将B(4,0)代入y= ![]() x+m,
x+m,
∴m=﹣2
∴直线BD的解析式为:y= ![]() x﹣2
x﹣2
联立 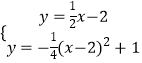
解得:x=4或x=﹣2
∴D(﹣2,﹣3)
∴由勾股定理可知:OD= ![]() ,BD=3
,BD=3 ![]() ,
,
设OB、OD、BD边上的高分别为h1,h2,h3,
∴h1=3
又∵OB=4,
∴S△BDO= ![]() OBh1=6,
OBh1=6,
∴ ![]() BDh3=
BDh3= ![]() ODh2=6,
ODh2=6,
∴h2= ![]() ,h3=
,h3= ![]() ,
,
∴△BDO三条高的和h1+h2+h3=3+ ![]() +
+ ![]()
(3)解:由题意可知:t=s2﹣s,
∵A(s,t)是y=ax2+bx+c(a≠0)的顶点,
∴y=a(x﹣s)2+t,
又因为该抛物线经过原点,
∴0=as2+t,
∴0=as2+s2﹣s,
∴s=(a+1)s2,
当s=0时,
此时,a全体实数,
当s≠0时,此时﹣1≤s<0或0<s<2,
∴a= ![]() ,
,
∴a≤﹣2或a>﹣ ![]() ,
,
综上所述,a≤﹣2或a>﹣ ![]()
【解析】(1)由题意可知A(2,1),设抛物线的解析式为y=a(x﹣2)2+1,由于抛物线过原点,所以将(0,0)代入即可求出a的值.(2)根据A(2,1)可求出OA的直线解析式,由于DB∥OA,所以一次项系数必定相等,从而可求出直线BD的解析式,联立直线BD与抛物线的解析式即可求出D的坐标,然后根据勾股定理分别求出OD、BD的长度,再求出BOD的面积即可求出△BDO三条高的和.(3)t=s2﹣s,由于A(s,t)是y=ax2+bx+c(a≠0)的顶点,所以y=a(x﹣s)2+t,将(0,0)代入该式后可得s=(a+1)s2 , 利用s的范围即可求出a的范围.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.