题目内容
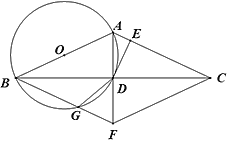
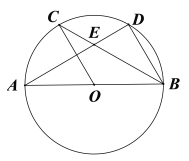
【题目】如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
(1)求证:![]() ;
;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
【答案】(1)证明见解析;(2)半径为![]() ;(3)PQ=
;(3)PQ=![]()
【解析】
(1)由等腰三角形的性质和平行线的性质可得∠OBC=∠CBD,即可证![]() ;
;
(2)通过证明△ACE∽△BCA,可得![]() ,可得AC=2,由勾股定理可求AB的长,即可求⊙O的半径;
,可得AC=2,由勾股定理可求AB的长,即可求⊙O的半径;
(3)过点O作OH⊥FQ于点H,连接OQ,通过证明△APC∽△CPB,可得![]() ,可求PA=
,可求PA=![]() ,即可求PO的长,通过证明△PHO∽△BCA,
,即可求PO的长,通过证明△PHO∽△BCA,
可求PH,OH的长,由勾股定理可求HQ的长,即可求PQ的长.
解:(1)∵OC=OB
∴∠OBC=∠OCB
∵OC∥BD
∴∠OCB=∠CBD
∴∠OBC=∠CBD
∴![]()
(2)连接AC,
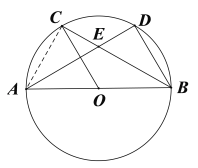
∵CE=1,EB=3,
∴BC=4
∵![]()
∴∠CAD=∠ABC,且∠ACB=∠ACB
∴△ACE∽△BCA
∴![]()
∴AC2=CBCE=4×1
∴AC=2,
∵AB是直径
∴∠ACB=90°
∴AB=![]() ,
,
∴⊙O的半径为![]() .
.
(3)如图,过点O作OH⊥FQ于点H,连接OQ,

∵PC是⊙O切线,
∴∠PCO=90°,且∠ACB=90°
∴∠PCA=∠BCO=∠CBO,且∠CPB=∠CPA
∴△APC∽△CPB
∴![]() ,
,
∴PC=2PA,PC2=PAPB
∴4PA2=PA×(PA+2![]() )
)
∴PA=![]() ,
,
∴PO=![]() ,
,
∵PQ∥BC
∴∠CBA=∠BPQ,且∠PHO=∠ACB=90°
∴△PHO∽△BCA
∴![]() ,
,
即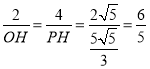 ,
,
∴PH=![]() ,OH=
,OH=![]() ,
,
∴HQ=![]() ,
,
∴PQ=PH+HQ=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目