题目内容
 如图,菱形ABCD的边长为4,∠B=120°,M为DC的中点,点N在AC上.
如图,菱形ABCD的边长为4,∠B=120°,M为DC的中点,点N在AC上.
(1)若DC=NC,则∠NDC=______度;
(2)若N是AC上动点,则DN+MN的最小值为______.
 解:(1)∵菱形ABCD的边长为4,∠B=120°,
解:(1)∵菱形ABCD的边长为4,∠B=120°,∴∠BCD=60°,∠ACB=∠ACD,
∴∠ACB=∠ACD=30°,
∵DC=NC,
∴∠CND=∠CDN,
∴
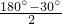 =75°;
=75°;(2)∵菱形ABCD的边长为4,∠B=120°,
∴∠BCD=60°,BC=CD,
∴△BCD是等边三角形,
∵D点关于AC的对称点为B点,连接BM交AC于点N,M为DC的中点,
∴BM⊥CD,DM=CM=2,
∴DN+MN=BM=BCsin60°=4×
 =2
=2 .
.故答案为:75;2
 .
.分析:(1)根据菱形的性质以及等腰三角形的性质得出∠CND=∠CDN,进而得出答案;
(2)首先根据菱形的性质得出△BCD是等边三角形以及连接BM后与AC的交点即为N点,进而利用锐角三角函数关系得出BM的长即可得出答案.
点评:此题主要考查了菱形的性质以及等边三角形的判定与性质和锐角三角函数的应用等知识,熟练利用菱形性质是解题关键.

练习册系列答案
相关题目
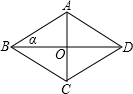 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
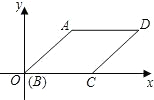 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.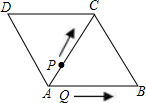 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).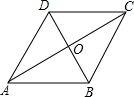 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.