题目内容
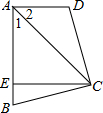 已知:如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且∠B+∠D=180°,求证:AE=AD+BE.
已知:如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且∠B+∠D=180°,求证:AE=AD+BE.分析:首先在AE上截取AM=AD,连接CM,再证明△AMC≌△ADC,可得∠3=∠D,再根据∠B+∠D=180°,∠3+∠4=180°,可以证出∠4=∠B,根据等角对等边可证出CM=BC,再根据等腰三角形的性质:等腰三角形底边上的高线与底边上的中线重合可得到ME-BE,再利用等量代换可证出AE=AD+BE.
解答: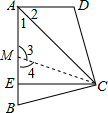 证明:在AE上截取AM=AD,连接CM,
证明:在AE上截取AM=AD,连接CM,
∵AC平分∠BAD,
∴∠1=∠2,
在△AMC和△ADC中
,
∴△AMC≌△ADC(SAS),
∴∠3=∠D,
∵∠B+∠D=180°,∠3+∠4=180°,
∴∠4=∠B,
∴CM=CB,
∵CE⊥AB,
∴ME=EB(等腰三角形底边上的高线与底边上的中线重合),
∵AE=AM+ME,
∴AE=AD+BE.
 证明:在AE上截取AM=AD,连接CM,
证明:在AE上截取AM=AD,连接CM,∵AC平分∠BAD,
∴∠1=∠2,
在△AMC和△ADC中
|
∴△AMC≌△ADC(SAS),
∴∠3=∠D,
∵∠B+∠D=180°,∠3+∠4=180°,
∴∠4=∠B,
∴CM=CB,
∵CE⊥AB,
∴ME=EB(等腰三角形底边上的高线与底边上的中线重合),
∵AE=AM+ME,
∴AE=AD+BE.
点评:此题主要考查了全等三角形的判定与性质,关键是正确做出辅助线,证出ME=BE.

练习册系列答案
相关题目
 39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
 已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC.
已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC. 已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2. 已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.