题目内容
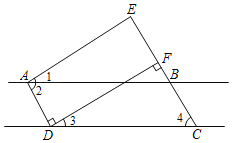
【题目】如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.
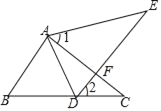
【答案】(1)见解析;(2)△ABD是等边三角形.理由见解析.
【解析】分析:
(1)由∠1=∠2结合∠AFE=∠DFC可得∠E=∠C,这样结合AE=AC,BC=DE即可证得△ABC≌△ADE,由此即可得到AB=AD;
(2)由∠1=∠2=60°可得∠BDE=120°,由△ABC≌△ADE可得∠B=∠ADE,AB=AD,进而可得∠B=∠ADB=∠ADE,由此即可得到∠ADB=![]() ∠BDE=60°,这样结合AB=AD即可得到△ABD是等边三角形.
∠BDE=60°,这样结合AB=AD即可得到△ABD是等边三角形.
详解:
(1)∵∠1+∠AFE+∠E=180°,∠2+∠CFD+∠C=180°,∠1=∠2,∠AFE=∠CFD,
∴∠E=∠C,
∵AC=AE,∠C=∠E,BC=DE,
∴△ABC≌△ADE,
∴AB=AD.
(2)△ABD是等边三角形.理由如下:
∵∠1=∠2=60°,
∴∠BDE=180°﹣∠2=120°,
∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠ADB,
∴∠ADB=∠ADE,
∴∠ADB=![]() ∠BDE=60°,
∠BDE=60°,
∴△ABD是等边三角形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生?
(2) 身高在 ![]() 到
到 ![]() 的女生有多少人?
的女生有多少人?
(3) 一女生的身高恰好为 ![]() ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少?