题目内容
【题目】按要求回答问题:
(1)已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;
(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则 ![]() 的值是多少?(直接写出结论,不要求写解答过程)
的值是多少?(直接写出结论,不要求写解答过程)
【答案】
(1)
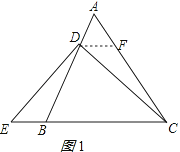
证明:作DF∥BC交AC于F,如图1所示:
则∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,
∵△ABC是等腰三角形,∠A=60°,
∴△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∴∠DBE=120°,∠ADF=∠AFD=60°=∠A,
∴△ADF是等边三角形,∠DFC=120°,
∴AD=DF,
∵∠DEC=∠DCE,
∴∠FDC=∠DEC,ED=CD,
在△DBE和△CFD中,  ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD;
(2)
解:EB=AD成立;理由如下:作DF∥BC交AC的延长线于F,如图2所示:

同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,
又∵∠DBE=∠DFC=60°,
∴在△DBE和△CFD中,  ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD
(3)
解: ![]() =
= ![]() ;理由如下: 作DF∥BC交AC于F,如图3所示:
;理由如下: 作DF∥BC交AC于F,如图3所示:

同(1)得:△DBE≌△CFD(AAS),
∴EB=DF,
∵△ABC是等腰直角三角形,DF∥BC,
∴△ADF是等腰直角三角形,
∴DF= ![]() AD,
AD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
【解析】(1)作DF∥BC交AC于F,由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;(2)作DF∥BC交AC的延长线于F,同(1)证出△DBE≌△CFD,得出EB=DF,即可得出结论;(3)作DF∥BC交AC于F,同(1)得:△DBE≌△CFD,得出EB=DF,证出△ADF是等腰直角三角形,得出DF= ![]() AD,即可得出结果.本题是三角形综合题目,考查了等边三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质、等腰直角三角形的判定与性质、平行线的性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.
AD,即可得出结果.本题是三角形综合题目,考查了等边三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质、等腰直角三角形的判定与性质、平行线的性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发现:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=﹣x2+40x;乙级干果从开始销售至销售的第t天的总销量y2(千克)与t的关系为y2=at2+bt,且乙级干果的前三天的销售量的情况见下表:
t | 1 | 2 | 3 |
y2 | 21 | 44 | 69 |
(1)求a、b的值;
(2)若甲级干果与乙级干果分别以8元/千克和6元/千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克? (说明:毛利润=销售总金额﹣进货总金额.这批干果进货至卖完的过程中的损耗忽略不计)