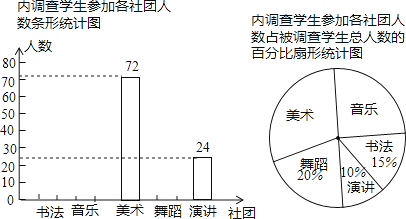
题目内容
【题目】如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 ![]() 上一点,BD交AC于点E,若BC=4,AD=
上一点,BD交AC于点E,若BC=4,AD= ![]() ,则AE的长是( )
,则AE的长是( ) 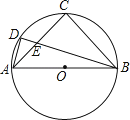
A.3
B.2
C.1
D.1.2
【答案】C
【解析】解:∵等腰Rt△ABC,BC=4,∴AB为⊙O的直径,AC=4,AB=4 ![]() ,
,
∴∠D=90°,
在Rt△ABD中,AD= ![]() ,AB=4
,AB=4 ![]() ,
,
∴BD= ![]() ,
,
∵∠D=∠C,∠DAC=∠CBE,
∴△ADE∽△BCE,
∵AD:BC= ![]() :4=1:5,
:4=1:5,
∴相似比为1:5,
设AE=x,
∴BE=5x,
∴DE= ![]() ﹣5x,
﹣5x,
∴CE=28﹣25x,
∵AC=4,
∴x+28﹣25x=4,
解得:x=1.
故选:C.
【考点精析】本题主要考查了三角形的外接圆与外心的相关知识点,需要掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目