题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把
,点E在边AB上,点F是边BC上不与点B、C重合的一个动点,把![]() 沿EF折叠,点B落在点
沿EF折叠,点B落在点![]() 处.若
处.若![]() ,当
,当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为__________.
的长为__________.

【答案】16或10
【解析】
等腰三角形一般分情况讨论:(1)当DB'=DC=16;(2)当B'D=B'C时,作辅助线,构建平行四边形AGHD和直角三角形EGB',计算EG和B'G的长,根据勾股定理可得B'D的长;
∵四边形ABCD是矩形,
∴DC=AB=16,AD=BC=18.
分两种情况讨论:
(1)如图2,当DB'=DC=16时,即△CDB'是以DB'为腰的等腰三角形
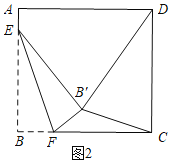
(2)如图3,当B'D=B'C时,过点B'作GH∥AD,分别交AB与CD于点G、H.

∵四边形ABCD是矩形,
∴AB∥CD,∠A=90°
又GH∥AD,
∴四边形AGHD是平行四边形,又∠A=90°,
∴四边形AGHD是矩形,
∴AG=DH,∠GHD=90°,即B'H⊥CD,
又B'D=B'C,
∴DH=HC=![]() ,AG=DH=8,
,AG=DH=8,
∵AE=3,
∴BE=EB'=AB-AE=16-3=13,
EG=AG-AE=8-3=5,
在Rt△EGB'中,由勾股定理得:
GB′=![]() ,
,
∴B'H=GH×GB'=18-12=6,
在Rt△B'HD中,由勾股定理得:B′D=![]()
综上,DB'的长为16或10.
故答案为: 16或10

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目






