题目内容
已知关于x的方程x2+4x+3k-1=0的两实根的平方和不小于这两个根的积;反比例函数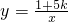 的图象的两个分支在各自的象限内,点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.
的图象的两个分支在各自的象限内,点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.
解:由题意,方程x2+4x+3k-1=0有实根,故△=16-4(3k-1)≥0,
解得k≤ ,
,
设方程两根为x1,x2,则有x1+x2=-4,x1x2=3k-1.
∵x12+x22≥x1x2.即:(x1+x2)2-3x1x2≥0,
即(-4)2-3(3k-1)≥0,
解得k≤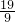 .
.
又由比例函数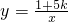 ,当x>0或x<0时,y随x增大而减小,可知:1+5k>0,即k>-
,当x>0或x<0时,y随x增大而减小,可知:1+5k>0,即k>- ,
,
所以k的取值范围为: ≥k>-
≥k>- ,
,
所以满足题中条件的k可取整数0和1.
分析:本题根据题中所给条件,列出关于K的不等式:△=16-4(3k-1)≥0,(x1+x2)2-3x1x2≥0,1+5k>0,解不等式组即可解得k的取值范围.
点评:本题考查了根与系数的关系及反比例函数性质,难度较大,关键根据题意列出关于K的不等式.
解得k≤
 ,
,设方程两根为x1,x2,则有x1+x2=-4,x1x2=3k-1.
∵x12+x22≥x1x2.即:(x1+x2)2-3x1x2≥0,
即(-4)2-3(3k-1)≥0,
解得k≤
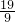 .
.又由比例函数
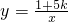 ,当x>0或x<0时,y随x增大而减小,可知:1+5k>0,即k>-
,当x>0或x<0时,y随x增大而减小,可知:1+5k>0,即k>- ,
,所以k的取值范围为:
 ≥k>-
≥k>- ,
,所以满足题中条件的k可取整数0和1.
分析:本题根据题中所给条件,列出关于K的不等式:△=16-4(3k-1)≥0,(x1+x2)2-3x1x2≥0,1+5k>0,解不等式组即可解得k的取值范围.
点评:本题考查了根与系数的关系及反比例函数性质,难度较大,关键根据题意列出关于K的不等式.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目