题目内容
（2007•西城区二模）已知关于x的方程x2+3x=8-m有两个不相等的实数根．
（1）求m的最大整数是多少？
（2）将（1）中求出的m值，代入方程x2+3x=8-m中解出x的值．
（1）求m的最大整数是多少？
（2）将（1）中求出的m值，代入方程x2+3x=8-m中解出x的值．
分析：（1）根据△=b2-4ac，易得-4m+41＞0，解不等式可得m＜
，进而可求m的最大整数值是10；
（2）把m=10代入方程中，解关于x的方程，可得x1=-1，x2=-2．
| 41 |
| 4 |
（2）把m=10代入方程中，解关于x的方程，可得x1=-1，x2=-2．
解答：解：（1）由于方程x+3x-8+m=0有两个不相等的实数根，
所以，b2-4ac=32-4×1×（-8+m）=-4m+41＞0，有m＜
，
故m的最大整数是10；
（2）当m=10时，原方程是x+3x+2=0，解得x=-2，x=-1．
所以，当m=10时，原方程的根是x1=-1，x2=-2．
所以，b2-4ac=32-4×1×（-8+m）=-4m+41＞0，有m＜
| 41 |
| 4 |
故m的最大整数是10；
（2）当m=10时，原方程是x+3x+2=0，解得x=-2，x=-1．
所以，当m=10时，原方程的根是x1=-1，x2=-2．
点评：本题考查了根的判别式、因式分解法求方程的根，解题的关键是先求出m的取值范围．
练习册系列答案
高中必刷题系列答案
相关题目
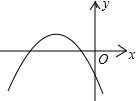（2007•西城区二模）已知二次函数y=ax2+bx+c的图象如图所示，下列结论：
（2007•西城区二模）若等边△ABC的边长为6cm长，内切圆O分别切三边于D、E、F，则阴影部分的面积是（ ）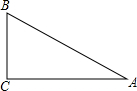
（2007•西城区二模）如图，在Rt△ABC中，斜边AB=8，∠B=60°，将△ABC绕点B旋转60°，顶点C运动的路线长是（ ）
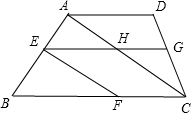（2007•西城区二模）如图，已知AD∥EG∥BC，且AC∥EF，记∠EFB=α，则图中等于α的角（不包含∠EFB）的个数为（ ）