题目内容
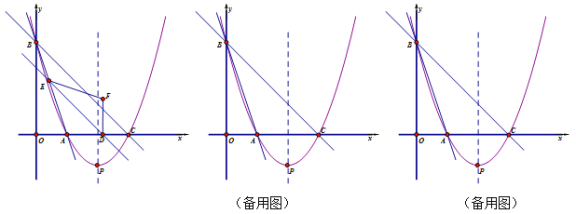
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,对称轴为直线x=2的抛物线经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一点Q,使△ABQ是以AB为底边的等腰三角形,求Q点的坐标;
(3)在直线BC的下方的抛物线上有一动点M,其横坐标为m,△MBC的面积为S,求S关于m的函数关系式,并求S的最大值及此时点M的坐标;
(4)平行于BC的动直线分别交△ABC的边AC、AB与点D、E,将△ADE沿DE翻折,得到△FDE,设DE=x,△FDE与△ABC重叠部分的面积为y,直接写出y与x的函数关系式及自变量x的取值范围.
【答案】(1)y=![]() (2)(2,2);(3)(
(2)(2,2);(3)(![]() )(4)y=
)(4)y=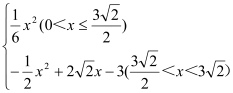
【解析】
试题分析:(1)先求出直线y=-3x+3与x轴交点A,与y轴交点B的坐标,再将A、B两点坐标代入y=a(x-2)2+k,得到关于a,k的二元一次方程组,解方程组即可求解;
(2)设Q点的坐标为(2,m),对称轴x=2交x轴于点F,过点B作BE垂直于直线x=2于点E.在Rt△AQF与Rt△BQE中,用勾股定理分别表示出AQ2=AF2+QF2=1+m2,BQ2=BE2+EQ2=4+2,由AQ=BQ,得到方程1+m2=4+2,解方程求出m=2,即可求得Q点的坐标;
(3)当点N在对称轴上时,由NC与AC不垂直,得出AC为正方形的对角线,根据抛物线的对称性及正方形的性质,得到M点与顶点P(2,-1)重合,N点为点P关于x轴的对称点,此时,MF=NF=AF=CF=1,且AC⊥MN,则四边形AMCN为正方形,在Rt△AFN中根据勾股定理即可求出正方形的边长.
(4)根据三角形的面积和相似三角形的性质,根据不同的范围可列函数的解析式.
试题解析:(1)∵直线y=﹣3x+3与x轴、y轴分别交于点A、B,∴A(1,0),B(0,3).
又∵抛物线的对称轴为直线x=2,∴抛物线与x轴的另一个交点C的坐标为(3,0),
设抛物线的解析式为y=a(x-1)(x-3),∵抛物线经过点B(0,3),
∴3a=3,解得a=1,故抛物线的解析式为y=![]() ;
;
(2)设Q点的坐标为(2,e),对称轴x=2交x轴于点T,过点B作BR垂直于直线x=2于点R.在Rt△AQT中,AQ2=AT2+QT2=1+e2,在Rt△BQR中,BQ2=BR2+RQ2=4+(3﹣e)2,
∵AQ=BQ,∴1+e2=4+(3﹣e)2,∴e=2,∴Q点的坐标为(2,2);
(3)过点M作MN∥y轴交直线BC于点N,![]() ,M(m,
,M(m,![]() )(0﹤m﹤3),
)(0﹤m﹤3),
N(m,-m+3),MN=-m+3-(![]() )=
)=![]() ,∴S=
,∴S=![]() ,当m=
,当m=![]() ,此时M(
,此时M(![]() ).
).
⑷依题意得△CBA面积为3,BC=![]() .当点F在BC上时,AF⊥BC,且AF=
.当点F在BC上时,AF⊥BC,且AF=![]() ,此时x=DE=
,此时x=DE=![]() ,所以分种情况考虑,①当0<x≤
,所以分种情况考虑,①当0<x≤![]() 时,△ADE≌△FDE,△ADE∽△ACB,而
时,△ADE≌△FDE,△ADE∽△ACB,而![]() ,计算得
,计算得![]() .②当
.②当![]() <x<
<x<![]() 时,连结AF交ED于K、交BC于G,EF交BC于H,DF交BC于I,由△ADE∽△ACB求得FK=AK=
时,连结AF交ED于K、交BC于G,EF交BC于H,DF交BC于I,由△ADE∽△ACB求得FK=AK=![]() ,FG=
,FG=![]() ,再由△FHI∽△FED得
,再由△FHI∽△FED得![]() ,∴
,∴![]() .
.
∴y=![]()
综上所述,函数关系式为y=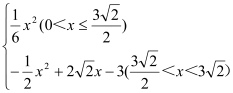

【题目】为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
用水量 | 单价 |
不超过6m3 的部分 | 2元/ m3 |
超过6m3不超过10m3的部分 | 4元/m3 |
超出10m3的部分 | 8元/m3 |
譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9-6)=24(元)
(1)某用户3月用水15 m3应缴水费多少元?
(2) 已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3) 如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?





