Question

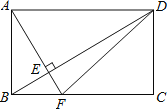
【题目】（本题满分7分）已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的作直线EF⊥BD分别交AD，BC于E，F两点，连结BE，DF．求证：四边形BFDE为菱形．

Answer 1

【答案】证明见解析

【解析】

试题分析：由四边形ABCD是平行四边形，即可得AD∥BC，OB=OD，易证得△DOE≌△BOF，可得DE=BF，即可正当四边形BEDF是平行四边形，又由EF⊥DB，即可证得平行四边形BEDF是菱形.

试题解析：∵四边形ABCD是平行四边形

∴AD∥BC，OB=OD

∵∠EDO=∠FBO,∠OED=∠OFB

∴△DOE≌△BOF（AAS），

∴OE=OF，

又∵ED∥BF

∴四边形BFDE为平行四边形.

又∵EF⊥BD，

∴四边形BFDE为菱形．