题目内容
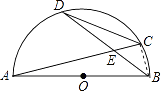
【题目】半圆O的直径AB=9,两弦AC、BD相交于点E,弦CD= ![]() ,且BD=7,则DE=
,且BD=7,则DE=
【答案】3 ![]()
【解析】根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=7-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴ ![]() ;
;
设BE=x,则DE=7-x,EC= ![]() x,AE=
x,AE= ![]() (7-x);
(7-x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=x,EC= ![]() x,则BC=
x,则BC= ![]() x;
x;
在Rt△ABC中,AC=AE+EC= ![]() -
- ![]() x,BC=
x,BC= ![]() x;
x;
由勾股定理,得:AB2=AC2+BC2,
即:92=( ![]() -
- ![]() x)2+(
x)2+( ![]() x)2,
x)2,
整理,得x2-14x+31=0,
解得:x1=7+3 ![]() (不合题意舍去),x2=7-3
(不合题意舍去),x2=7-3 ![]()
则DE=7-x=3![]() .
.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目