题目内容
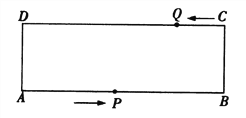
【题目】如图,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A,B,C,D分别在l1,l2,l3,l4上,过点D作DE⊥l1于点E,已知相邻两条平行线之间的距离为1,求AE及正方形ABCD的边长.

【答案】AE=1,AD=![]() .
.
【解析】
过点B作BF⊥l1,垂足为点F,由正方形的性质可得出∠BAD=90°,AB=AD,再由垂直可得出∠BFA=∠AED=90°,通过角的计算得出∠EAD=∠FBA,由此即可证出△FAB≌△EDA(AAS),根据全等三角形的性质以及勾股定理即可求出AE、AD的长度.
过点B作BF⊥⊥l1,垂足为点F,如图所示.

∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD,
∵BF⊥l1,DE⊥l1,
∴∠FAB+∠EAD=90°,∠FAB+∠FBA=90°,∠BFA=∠AED=90°,
∴∠EAD=∠FBA,
在△FAB和△EDA中,
 ,
,
∴△FAB≌△EDA(AAS),
∴AE=BF=1,
∵ED=2,
∴AD=![]() =
=![]() .
.

 中考解读考点精练系列答案
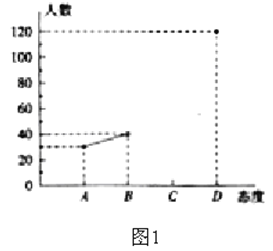
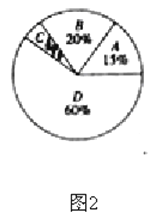
中考解读考点精练系列答案【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
【题目】某校开展了“让世界充满爱”的捐款助学活动,其中八(2)班全体同学的捐款情况如下表:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 12 | 3 |
由于填表的同学不小心把墨水滴在了表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的36%,结合上表回答下列问题:
(1)八(2)班共有多少人?
(2)学生捐款金额的众数和中位数分别为多少元?
(3)如果把该班学生的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对应的扇形圆心角为多少度?