题目内容
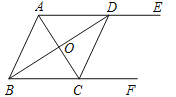
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
【答案】(1)90°;(2)证明见解析.
【解析】
试题分析:(1)首先根据角平分线的性质得到∠DAC=∠BAC,∠ABD=∠DBC,然后根据平行线的性质得到∠DAB+∠CBA=180°,从而得到∠BAC+∠ABD=![]() (∠DAB+∠ABC)=
(∠DAB+∠ABC)=![]() ×180°=90°,得到答案∠AOD=90°;
×180°=90°,得到答案∠AOD=90°;
(2)根据平行线的性质得出∠ADB=∠DBC,∠DAC=∠BCA,根据角平分线定义得出∠DAC=∠BAC,∠ABD=∠DBC,求出∠BAC=∠ACB,∠ABD=∠ADB,根据等腰三角形的判定得出AB=BC=AD,根据平行四边形的判定得出四边形ABCD是平行四边形,即可得出答案.
试题解析:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∵AE∥BF,∴∠DAB+∠CBA=180°,∴∠BAC+∠ABD=![]() (∠DAB+∠ABC)=
(∠DAB+∠ABC)=![]() ×180°=90°,∴∠AOD=90°;
×180°=90°,∴∠AOD=90°;
(2)证明:∵AE∥BF,∴∠ADB=∠DBC,∠DAC=∠BCA,∵AC、BD分别是∠BAD、∠ABC的平分线,∴∠DAC=∠BAC,∠ABD=∠DBC,∴∠BAC=∠ACB,∠ABD=∠ADB,∴AB=BC,AB=AD
∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形,∵AD=AB,∴四边形ABCD是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目